How do the methods for calculating grounding device resistance differ?

To calculate the resistance of a grounding device (GD), design engineers refer to reference guides containing formulas for calculating the resistance to current dissipation of different types of grounding electrodes. A misconception has arisen that a particular source contains the "correct" or "incorrect" version of the grounding resistance formula and that the formulas not only look different but will also provide different results. Designers tend to use a specific reference material, become accustomed to it, and often vigorously defend their preferred formula variant. The purpose of this article is to refute this erroneous preference; we will prove that any formulas for a specific type of grounding electrode are equivalent and will yield the same result.

Resistance to Current Dissipation of a Vertical Grounding Electrode

For a vertical grounding electrode, Barybin's "Reference Guide for the Design of Electrical Networks and Equipment," Table 7.9, uses a formula variant with a decimal logarithm:

RD 34.35.514-85 "Instructions for the Operation of Surge Protection Means," Table P15.4, provides a formula, but with a natural logarithm:

This same formula is also given in the Reference Guide by Karyakin "Grounding Devices of Electrical Installations," Table 3.8, row 6; the Reference Guide by Mankov "Protective Grounding and Protective Neutralization of Electrical Installations," Table 7.21; the Reference Guide by Basmanov "Grounding and Lightning Protection," Table 4.1; and the Reference Guide by Dolin "Fundamentals of Safety in Electrical Installations," Table 3.1.
In mathematics, the following equality is known: ln(X)=In10*lg(X). Therefore, the value ln10 can be factored out of the formula from RD 153-34.3-35.125-99, after which the expression in parentheses contains decimal logarithms (lg) instead of natural logarithms (ln), making the expression identical to the one in Barybin's Reference Guide:

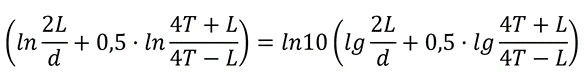
The value ln10 factored out is equal to 2.3, and after dividing 2.3 by 2π, we get 0.366—the constant present in the formula from Barybin's Reference Guide. The expressions outside the parentheses also turn out to be identical. As a result, the formula from RD 153-34.3-35.125-99 takes the form of the formula from Barybin's Reference Guide:

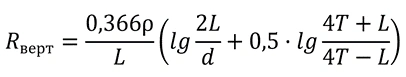
From this proof, it is clear that the formulas are identical; only their initial form of notation differs, so the calculation result will be the same.

Resistance to Current Dissipation of a Horizontal Grounding Electrode

Barybin's Reference Guide provides a formula with a decimal logarithm for calculating the resistance to current dissipation of a horizontal grounding electrode:

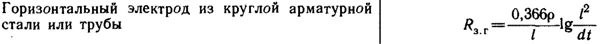
For a horizontal grounding electrode, RD 34.35.514-85 "Instructions for the Operation of Surge Protection Means," Table P15.4, provides a formula with a natural logarithm.

Let's apply the same steps to the horizontal ground electrode as we did for the vertical one. Starting from the formula in RD 34.35.514-85 and following the rule ln(X)=In(10)*lg(X), we factor the natural logarithm of 10 out of the parentheses:

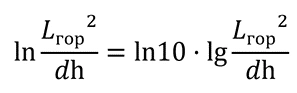
ln10 equals 2.3, and dividing 2.3 by 2π gives 0.366. Again, the expressions before the logarithm and inside it become absolutely identical:

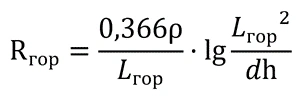
It can be concluded that the initial formulas are equivalent, and choosing any of them for the calculation will not affect the result.

Conclusion

As we have seen, different sources, although containing alternative forms of the formulas, do not affect the final result of the grounding resistance calculation. It has been proven that after elementary mathematical transformations, the formulas take on an identical form.

The ZANDZ Technical Center uses the more common form of the equation with the natural logarithm (ln) for calculations of vertical and horizontal grounding electrode but does not deny the correctness of performing calculations using the variant with the decimal logarithm (lg). The designer is free to choose any form of the formula.

Features, typical errors, and safety when measuring grounding resistance Guidelines for Measuring Resistance of a Grounding Arrangement Electrolytic Grounding in Permafrost Soils: Should Vertical of Horizontal Electrodes Be Used? Measuring the Earthing Resistance Using Conventional Three- and Four-Wire Methods