Пятый вебинар из серии "Заземление и молниезащита: вопросы и проблемы, возникающие при проектировании"
Текст вебинара. Страница 2
Быстрая навигация по слайдам:
1. Расчет заземляющих устройств
2. Заземляющие электроды
3. Расчет сопротивления заземления
4. Теория электрического поля постоянного тока
5. Основные соотношения, сопротивление заземления
6. Основные соотношения, две вычислительные проблемы
7. Уравнения для электродов
8. Можно ли считать по усредненной плотности тока утечки?
9. Пример расчетного алгоритма, п. 1-3
Страница 2:
10. Пример расчетного алгоритма, п. 4-8
11. Зеркальное отражение на границе грунт-воздух
12. Учет глубины верхнего конца электрода, стержень
13. Учет глубины верхнего конца электрода, шина
14. Влияние соседних заземляющих электродов
15. Сопротивление заземления с учетом взаимного влияния электродов
16. Упрощение расчета сопротивления заземления ж.б. свай и балок
17. Учет неравномерности распределения тока утечки по заземляющим электродам
18. Расстояние между электродами не меньше их длины
Пример расчетного алгоритма, п. 4-8
И дополнительное уравнение для тока. Когда вы все вместе решите, вы найдете напряжение неизвестное, поделите на ток, для которого вы считали и получите результат. Какая система уравнений получается для реальных вариантов? Для реальных вариантов получается вот какая система. Я взял контур заземления хорошего завода или подстанцию. Это, примерно, 250 метров в длину, 250 метров в ширину. И в этом контуре сделал ячейки, шагом квадратные, шагом 10 метров. Тогда количество тех самых электродов, которое у меня получилось, оно получилось, примерно, где-то на уровне 800 электродов. И уравнений, которое надо решать - это 800 уравнений. Сколько времени потратила простая современная персональная машина? Примерно, 20 секунд. Через 20 секунд я получаю ответ. Все, в общем, делать то, если говорить по совести, больше и нечего. Вроде бы и семинар надо закрывать, в таком случае.
Зеркальное отражение на границе грунт-воздух
Но вот какая раскладка, когда хочется как-то упростить ситуацию и всегда хочется рассмотреть приемы, которые дают возможности сделать оценки. И я хочу посмотреть эти приемы и показать вам, как можно получить, может быть, те расчетные соотношения, с которыми вы, вообще говоря, хорошо знакомы. Первый вариант, который я хочу посмотреть, вот какой. От поверхности земли вид электрода (рисунок слева), длины l. Как в этом случае поступать? А поступаем очень просто. Для того, чтобы убрать эту границу и посчитать, что электрод находится в однородном грунте и никакого воздуха на верху на самом деле нет, надо отразить электрод с таким коэффициентом отражения. Если учесть, что удельное сопротивление воздуха бесконечно велико, то этот коэффициент получается равным единице. Тогда у вас получается, что есть электрод удвоенной длины, вот такой, который надо подставить уже выведенную впереди формулу. А подставлять остается только одно единственное. Вместо длины фактической подставить длину ту , которая получилась, а получилась длина удвоенная. То есть вместо l надо подставить 2l. Если это я подставлю сюда, под логарифм и подставлю в знаменатель, то у меня получится такое выражение (формула внизу), правда без этой 2. Теперь, откуда взялась эта 2? Двойка то взялась вот откуда. Ведь на самом то деле работает не весь электрод, а его половина и поэтому сопротивление заземления получится в два раза больше, чем то, которое дает формула.
Учет глубины верхнего конца электрода, стержень
Следующий, более важный практический результат. Электрод забили вертикальный в грунт не от поверхности земли, а забили его в траншейке на глубине h. Тогда отражение получается таким: вот реальный электрод, а вот электрод, который отразился, для того, чтобы убрать эту границу и он находится друг от друга на двойной высоте h. Все формулы работают снова, все те же самые. Собственный потенциал, он какой был такой и остается, вот он. И надо добавить потенциал от отраженного электрода, имея в виду, что расстояние между началом этой штуки и этой точкой, оно равно вот такой величине. Вот, она. А расстояние между этой точкой и фактической расчетной точкой реального электрода, вот оно. Это простая геометрия. В результате полный потенциал складывается из потенциала собственного тока и с потенциала от отраженного тока. Этот полный потенциал здесь записан, остается это полный потенциал поделить на ток, получится выражение для сопротивления заземления. Это выражение для сопротивления заземления я специально записал в таком виде, в каком он записывается обычно в справочнике. Там используют такую величину, вводят некий расчетный параметр t равный длине пополам плюс эта глубина h. Получается такое расчетное соотношение, которое существует абсолютно во всех справочниках.
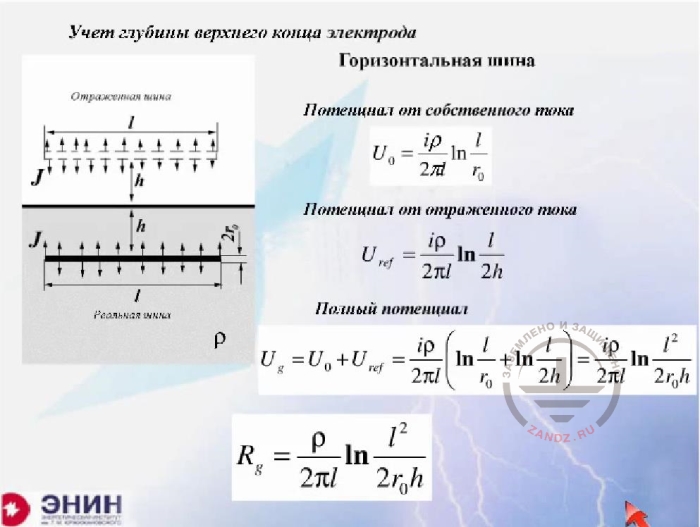
Учет глубины верхнего конца электрода, шина
Теперь точно такую же операцию можно проделать, если у вас заглублена шина, длины l, вот она шина длины l, на глубину h. Вот, потенциал от собственного тока шины, а вот потенциал от отраженного тока шины. Если я их сложу вмести, то получится, такое выражение, надо только к алгоритму привести. То есть те формулы, которые гуляют по справочникам получаются элементарно простым способом. если вы запомните только две вещи. Запомните выражение для потенциального коэффициента и запомните выражение для отраженного тока, который вы случае, когда отражается это отток в воздухе, отражение происходит с поправочным коэффициентом тождественно равным единице.
Влияние соседних заземляющих электродов
Теперь вопрос вот какой. Представьте себе, что у вас есть несколько электродов, которые расположены не слишком далеко один от другого. Например, я нарисовал здесь простейшую ситуацию, которая здесь есть. Когда у меня три электрода находятся в однородном грунте, границы нет никакой для простоты и эти электроды расположены в вершинах равностороннего треугольника. Теперь каждый электрод симметричен относительно всех других. Поэтому решать вопрос о токе здесь не приходится. Ток, который стекается с электродов с их полной симметрией, будет распределен равномерно между тремя электродами, и с каждого электрода будет растекаться на три тока. Я снова хочу посмотреть, какое будет сопротивление заземления в этом случае, когда у меня будут работать три электрода. Опять же потенциал от собственного тока одного электрода определяется вот таким выражением. А потенциал от соседних электродов определяется таким выражением, в которых вместо расстояния R здесь фигурирует это расстояние D.
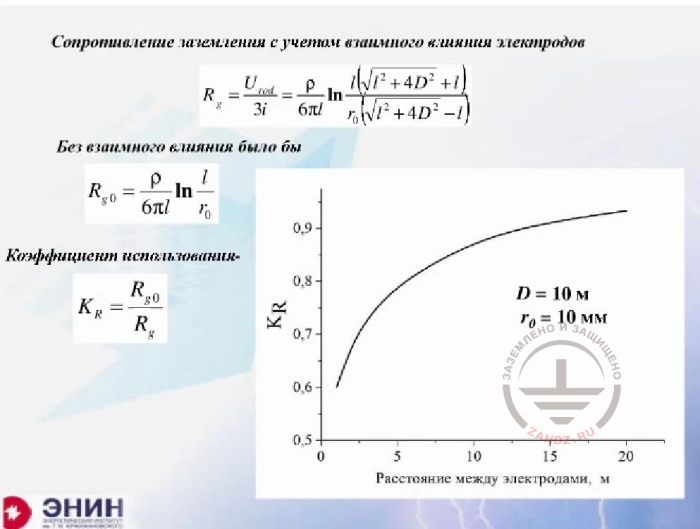
Сопротивление заземления с учетом взаимного влияния электродов
Сравнить выражение, которое я здесь записал внизу и которое мне дает сопротивление заземления фактически этой системы с тем, что получилось бы, если бы я читал, что каждый электрод как параллельный действует как независимый, тогда у меня сопротивление заземления получилось бы в три раза меньше, чем у уединенного электрода. И вот, это второе выражение. Теперь если это я поделю на это (первую формулу на вторую), то у меня получится тот проклятый коэффициент использования, который фигурирует во всех книжках. Поглядите, что у меня получается. Этот коэффициент использования зависит от расстояния между электродами и тот расчет, который я продела, он такой. Длина электродов по 10 метров, радиус электродов 10 мм, а расстояние между электродами меняется. И чем меньше это расстояние, тем меньше становится коэффициент использования. При расстоянии на уровне 1 м, этот коэффициент использования где-то на уровне 0, 6. То есть иными словами - я должен получить цифру, а потом разделили бы ее на коэффициент использования, в результате чего расчетного значения удвоилось бы. Спрашивается, если я виду какой-то расчет, а потом ввожу в этот расчет поправку, которая меняет расчетную величину вдвое, то возникает законный вопрос: а считаю то я что? Получается, что считаю я не очень грамотно и не очень правильно.
Упрощение расчета сопротивления заземления ж.б. свай и балок
Но особенно важна, вот какая штука. Когда расстояние между заземляющим и электродами очень маленькое, например, на уровне 10 см. Откуда возьмутся такие расстояния? Вообще говоря, никто, наверное, нет такого идиота инженера, который забьет стержни в грунт на расстоянии 10 см друг от друга. Правильно, такого нет. Зато у вас есть арматура фундамента, в которой находятся арматурные стержни. По нашему российскому законодательству арматуру фундамента используют в качестве заземляющих электродов и это стандартный типовой прием. И в этом стандартном типовом приеме сделана следующая вещь. В основе этого приема лежит очень большая работа НИИ железобетона, который показал, что бетон, когда он попадает в грунт, он всасывает влагу и через достаточное короткое время бетон ничем не отличается от того грунта, в котором он лежит. И значит, вы имеете арматурные стержни, которые лежат в этом бетоне на расстоянии где-нибудь там, на уровне каких-нибудь десятков сантиметров. Если вы возьмете, и посчитает коэффициент использования для этого случая. А я считал, например, такую вещь - стержни арматурные десятиметровой длины, радиус их 1 см, а расстояние между этими стержнями где-то на уровне 10 см, то коэффициент использования, который получается, он получается на уровне где-то 0,25. И получается, что тот результат, который вы получили бы, нужно было бы поправить в 2 с лишним раза. Но интересно вот что. Интересна вот такая вещь. Я провел расчет при этом расстоянии 10 см между стержнями, три стержня. Посчитал сопротивление заземления правильно грамотно, у меня получилась такая величина. Такой коэффициент, который надо умножить на удельное сопротивление грунта. А теперь я задаю вот какой вопрос. А каким должен был бы быть радиус стержня, который я заменил бы все эти три электрода и получил бы точно такую же величину. Я решаю эту задачу, она решается элементарно просто и получается, что в данном случае этот радиус равен 4,6 см. А что это такое 4,6 см? А это оказывается радиус окружности, на которой стоят эти самые стержни под углом 120 градусов. И получается вот какая вещь. Оказывается, что арматурные стержни, расположенные в любом количестве с равным шагом на заданной окружности, можно заменить одним единственным стержнем, радиус которого равен вот такой величине (последняя формула). Эта формула, которую я здесь написал, один в один соответствует формуле для расчета эквивалентного радиуса расщепленного провода, который используют на линии электропередачи для расчета емкостей. Значит можно не беспокоиться о сложном расчете, скажем, арматурной сваи. Нужно знать, сколько в ней арматурных стержней, нужно знать по какому среднему радиусу распределены эти стержни. Взять подставить это в расчетную формулу, получить эквивалентный радиус и дальше считать, что никакой сваи у вас нет, а есть просто одиночный стержень, вот такого радиуса.
Учет неравномерности распределения тока утечки по заземляющим электродам
Теперь более сложная задача. Более сложная задача, она будет вот какая. Когда у вас стержни расположены несимметрично. Смотрите, у меня набор из трех электродов: один, второй, третий. И теперь токи в этих электродах в крайних будут одинаковы, но в центральном электроде ток, вообще говоря, будет другой. И вопрос заключается в том: а такую систему можно каким-нибудь способом рассчитать и как ее рассчитывать? Оказывается, никакой проблемы здесь нет, потому что сумма токов всех трех стержней должна быть полному току равна. Ток двух крайних стержней, вот он. И теперь я записываю выражение для потенциала центрального стержня через потенциальные коэффициенты от крайних стержней и от своего собственного. А для среднего тоже через собственный и соседние потенциальные коэффициенты. Все эти потенциальные коэффициенты я уже показывал, как считать, они здесь расписаны. В результате я получаю примерно, такую штуку.
Расстояние между электродами не меньше их длины
Я получаю, что неравномерность распределения тока она зависит и это вполне естественно от того, на каком расстоянии находится стержень. Если эти десятиметровые стержни находятся, скажем, на расстоянии 1 м, как показано на этой самой верхней строчки. Если я возьму и запишу эти выражения для десятиметровых стержней на расстоянии метр, нагрузка будет действительно существенно различной. Смотрите, в крайних стержнях будет по 40% тока, а в центральном стержне будет 20% тока. Но если я начну разделять стержни на расстояние, которое практически используется, скажем, возьму между десятиметровыми стержнями, расстояние где-нибудь на уровне 5 метров, то у меня токовая нагрузка всех стержней окажется практически одинаковой.
<< Предыдущая страница
слайды с 1 по 9
Следующая страница >>
слайды с 19 по 22 + блок вопросов и ответов
Полезные материалы для проектировщиков:
- Вебинары с ведущими экспертами отрасли
- Все для расчетов заземления и молниезащиты
- Полезные материалы: статьи, рекомендации, примеры
Смотрите также:
 Молниезащита жилых и общественных зданий - ответы на частые вопросы при проектировании
Молниезащита жилых и общественных зданий - ответы на частые вопросы при проектировании
 УЗИП и его плавкая вставка
УЗИП и его плавкая вставка
 Молниезащита и заземление для базовых станций стандарта 5G
Молниезащита и заземление для базовых станций стандарта 5G
 Анализ нормативного документа ФЕДЕРАЛЬНЫЕ НОРМЫ И ПРАВИЛА В ОБЛАСТИ ПРОМЫШЛЕННОЙ БЕЗОПАСНОСТИ "ПРАВИЛА БЕЗОПАСНОСТИ ПРИ ВЗРЫВНЫХ РАБОТАХ"
Анализ нормативного документа ФЕДЕРАЛЬНЫЕ НОРМЫ И ПРАВИЛА В ОБЛАСТИ ПРОМЫШЛЕННОЙ БЕЗОПАСНОСТИ "ПРАВИЛА БЕЗОПАСНОСТИ ПРИ ВЗРЫВНЫХ РАБОТАХ"
 Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 1
Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 1
 Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 2
Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 2
 Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 3
Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 3