Когда не обойтись без схемы с распределёнными параметрами

4. Когда не обойтись без схемы с распределёнными параметрами

Четвёртая часть статьи "Методика расчёта токов нагрузки УЗИП"

Как это не удивительно, но речь пойдёт не о воздушных линиях электропередачи, а о протяженных подземных коммуникациях. Это могут быть, например, металлические трубопроводы или просто очень длинные заземляющие шины. Погонная индуктивность такой коммуникации примерно такая же, как у ВЛ. Не так уж сильно вырастает и погонная ёмкость (относительная диэлектрическая проницаемость грунта ε, как правило, не больше 10) и потому ёмкостный ток утечки в грунт во многих практических ситуациях намного меньше тока в заземляющих устройствах. Но кондуктивная погонная поперечная проводимость, определяющая утечку тока молнии через поверхность контакта коммуникации с грунтом, очень значительна. Как известно, сопротивление заземления горизонтальной шины радиусом r₀ и длиной l, проложенной в грунте с удельным сопротивлением ρ на глубине h, равно

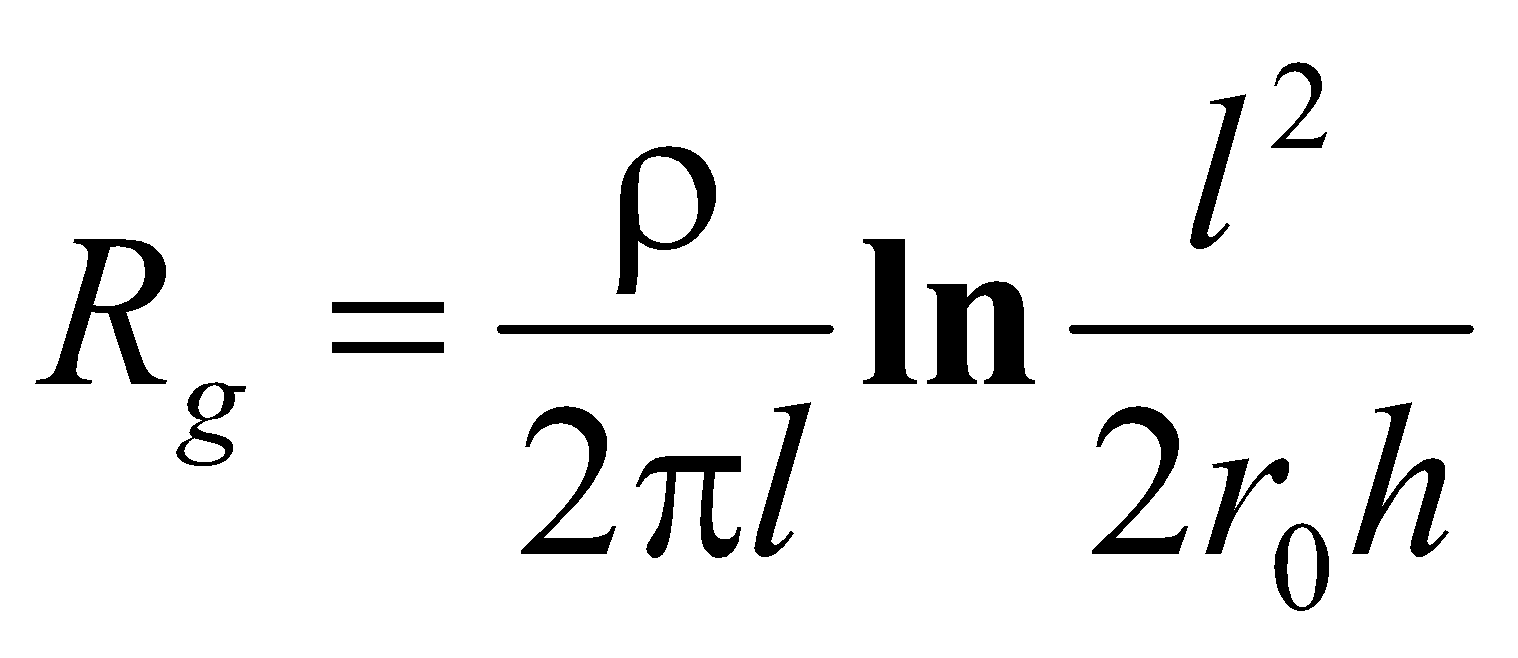
, (17)

Например, при длине 200 м и радиусе 5 см металлическая труба в грунте с ρ =100 Ом м при глубине заложения 1 м будет обладать сопротивлением заземления около 1 Ом. Это сопоставимо не только с сопротивлением заземления защищаемого объекта, но даже с типичным сопротивлением заземления ПС. Ясно, что столь значимый параметр необходимо учитывать в расчёте.

Теперь стоит вспомнить, как осуществлялся переход от схемы замещения с распределенными параметрами к сосредоточенной схеме. Фактически вместо большого числа коротких расчётных отрезков дело ограничилось единственным, длина которого равнялась длине коммуникации, а индуктивность – её полной индуктивности. Роль индуктивности принципиально не изменилась. Как и в схеме с распределёнными параметрами она разделяет сопротивления заземления по концам коммуникации. Что же касается ёмкости коммуникации, то ею пренебрегалось, поскольку ток утечки через ёмкость был пренебрежимо мал по сравнению с током через сопротивления заземления. Для подземного кабеля, как только что было показано, наиболее значима как раз не ёмкостная, а кондуктивная утечка. Это благодаря ей коммуникация может иметь очень низкое сопротивление заземления. Конечно, можно попытаться отобразить его дополнительными резисторами, включенными параллельно сопротивлениям по концам коммуникации, как это показано на рис. 11. Но поскольку введённые резисторы R_g сопоставимы с сопротивлениями заземления R₁ и R₂, режим распределения тока будет очень резко искажен. Иллюстрацией могут служить расчётные данные на рис. 12.

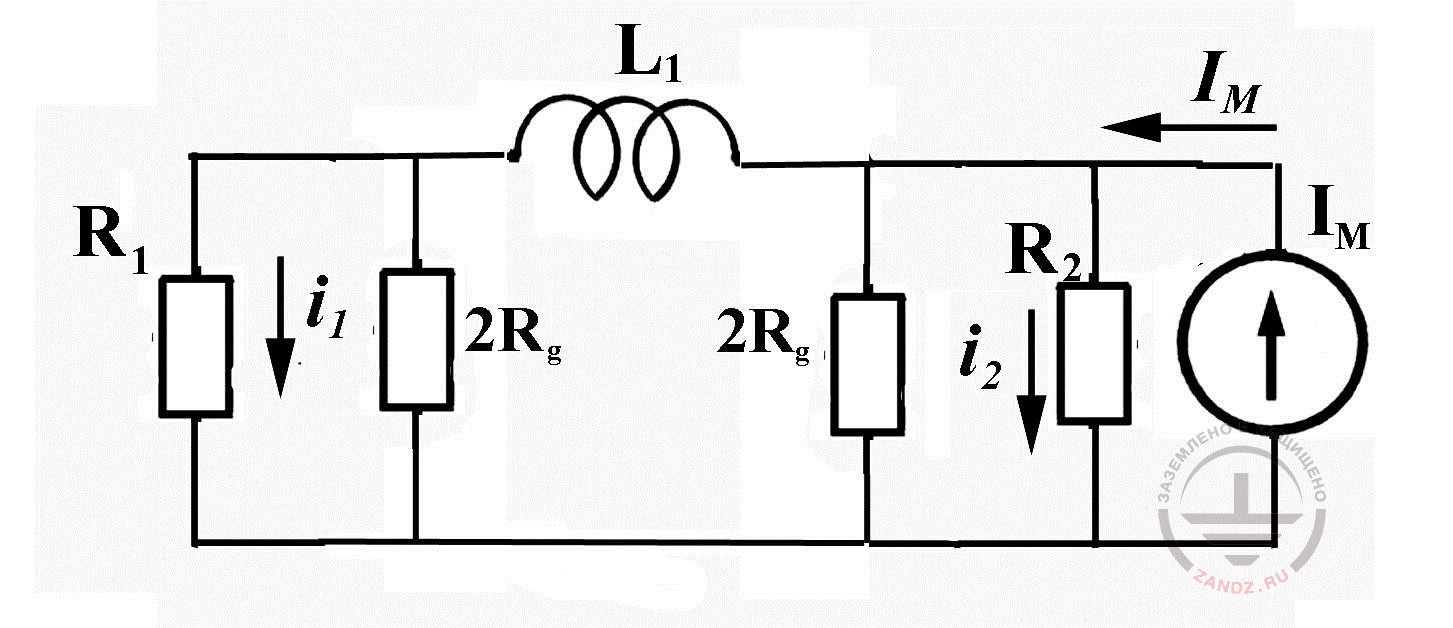
Рис. 11. К обоснованию схемы замещения подземной коммуникации в проводящем грунте.

Они получены расчётом по схеме с сосредоточенными параметрами (рис. 11) для трубопровода длиной 200 м и радиусом 5 см. Предполагалось, что он уложен в грунт удельным сопротивлением 100 Ом м на глубину 0,5 м. Сопротивление заземления объекта, пораженного молнией, принято равным 10 Ом, сопротивление на другом конце трубопровода - 1 Ом. Для сравнения на рис. 12 нанесены также расчётные значения токов, полученные в схеме замещения с распределёнными параметрами. Общего между ними очень немного. Ясно, что здесь не избежать строгого расчёта.

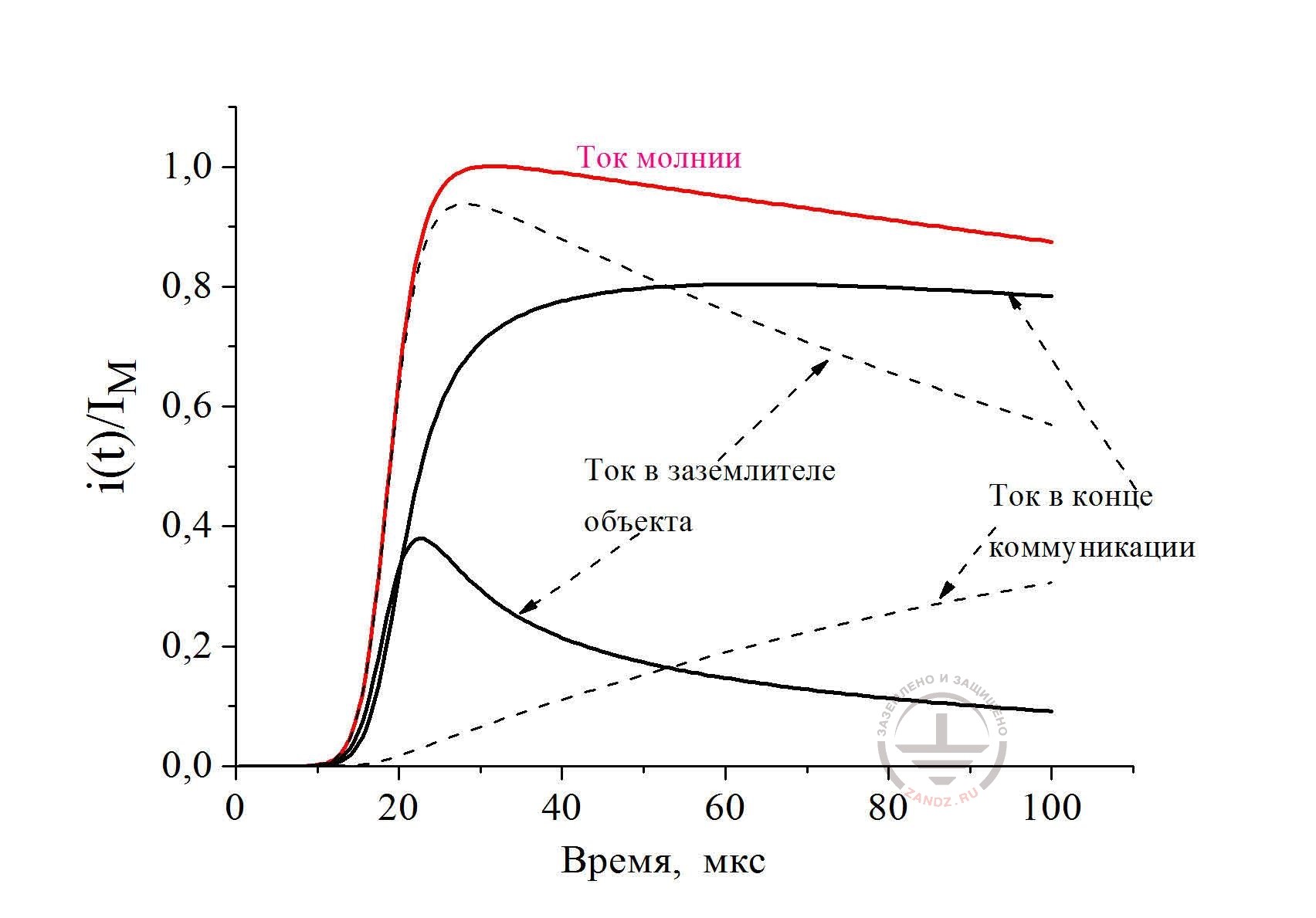
Рис. 12. Сопоставление результатов расчета распределения тока молнии при наличии подземного трубопровода длиной 200 м между сосредоточенными заземлителями в схеме замещения с распределенными (сплошные кривые) и сосредоточенными параметрами (штрих. кривые).

В большинстве практических ситуаций, когда удается пренебречь ёмкостной утечкой тока по сравнению с кондуктивной утечкой, система уравнений в частных производных приобретает вид

;
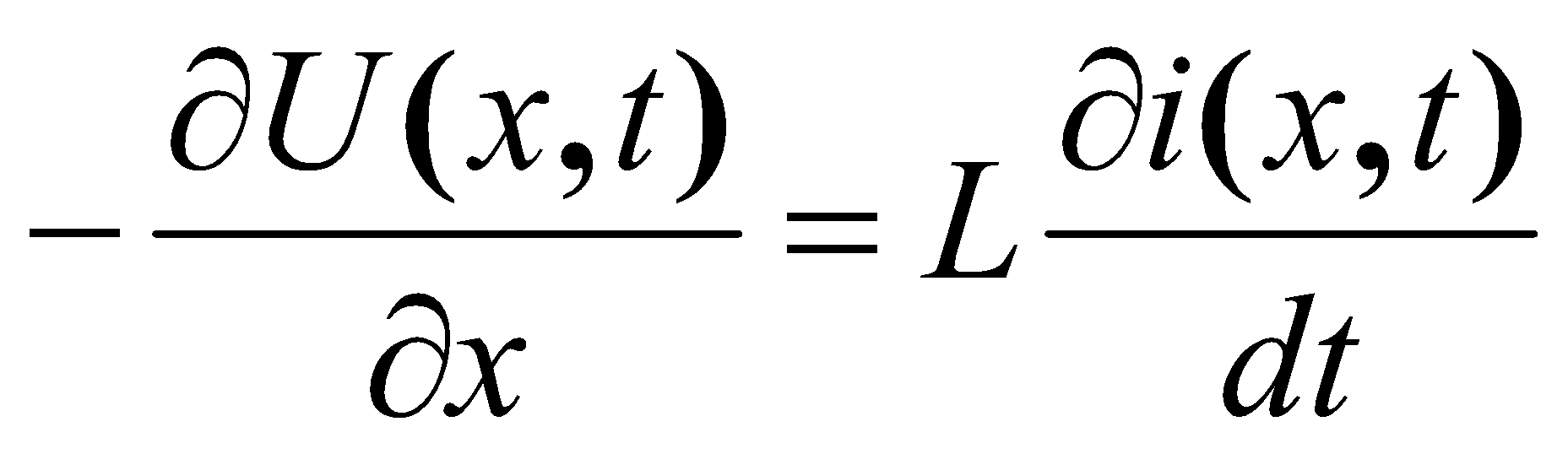
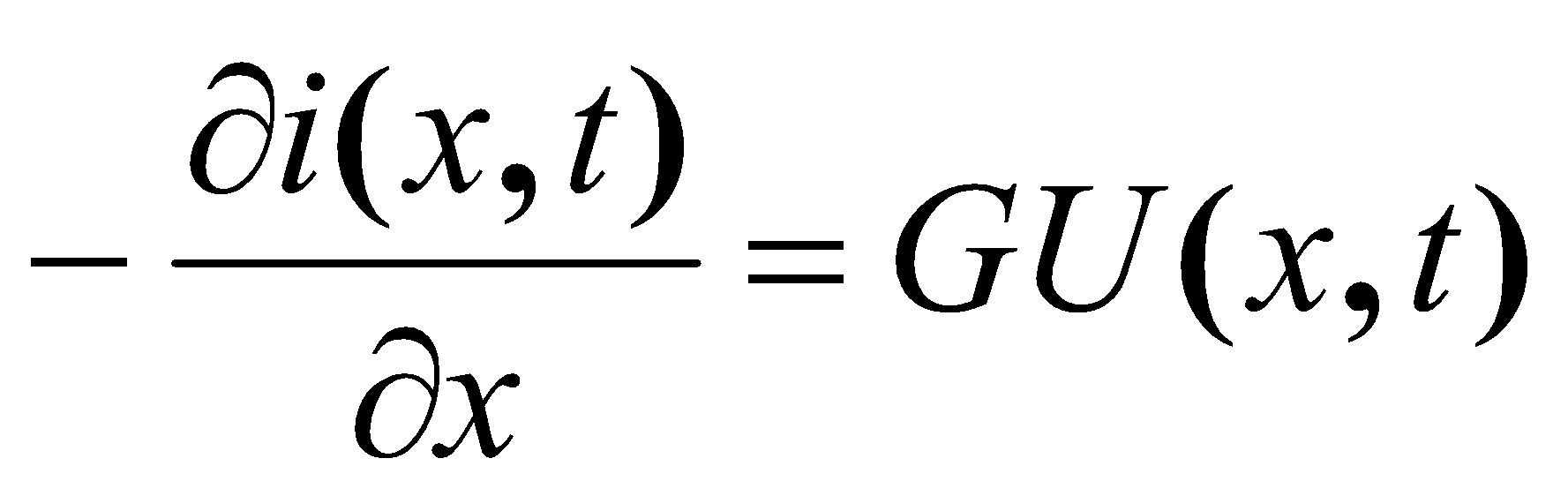
(18)

и повторным дифференцированием по x приводится к известному уравнению диффузии

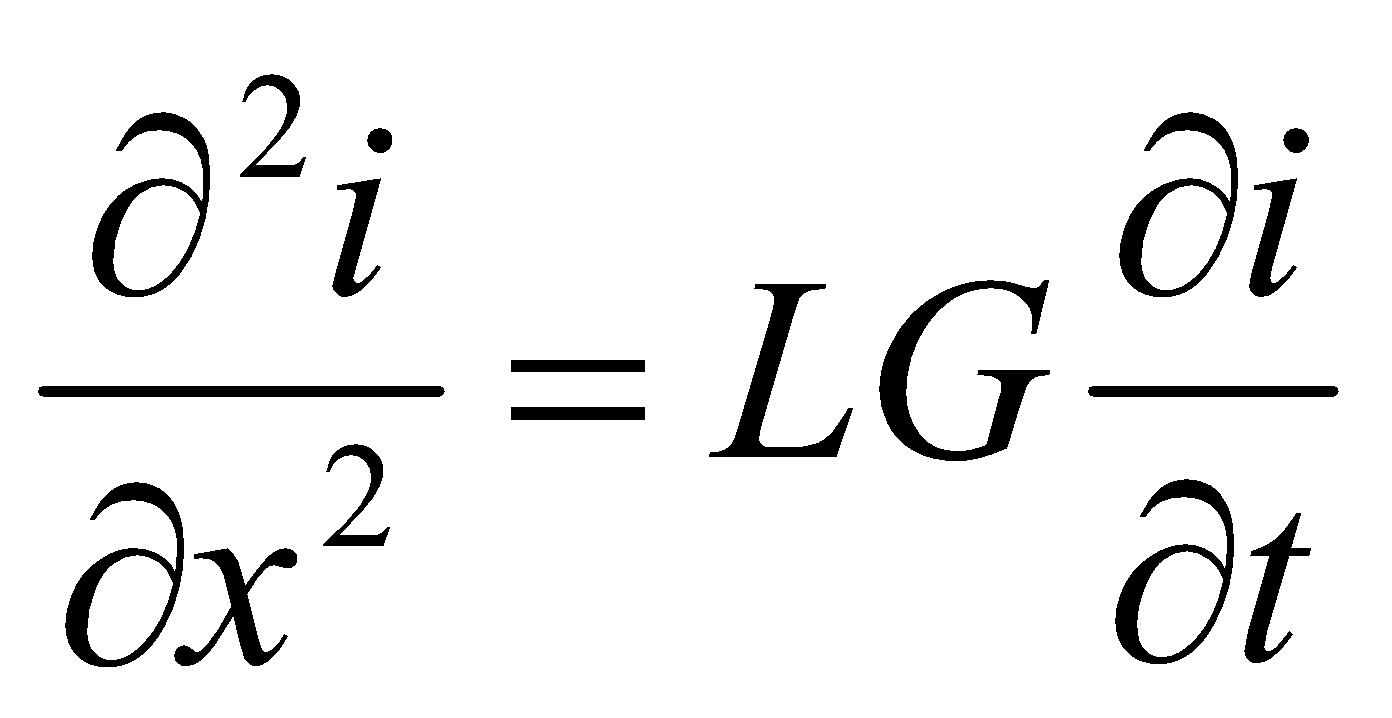
(19)

Здесь G – погонная проводимость утечки в грунт, а погонное сопротивление подземной коммуникации R вследствие его малости из уравнений исключено. Алгоритм численного решения уравнения (19) ничем не отличается от рассмотренного в разделе 3 для участка ВЛ. Только в этом случае удобнее сначала прямой прогонкой определить токи в продольных отрезках подземной коммуникации, а затем обратной прогонкой вычислить напряжения отрезков.
Для прямой прогонки используется разностное выражение

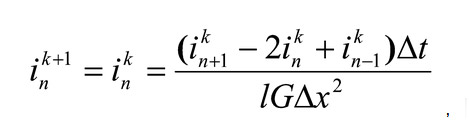
формула 20

(20)

При этом ток в последнем N-ом отрезке коммуникации, связанной с заземлителем R_k, вычисляется по выражению

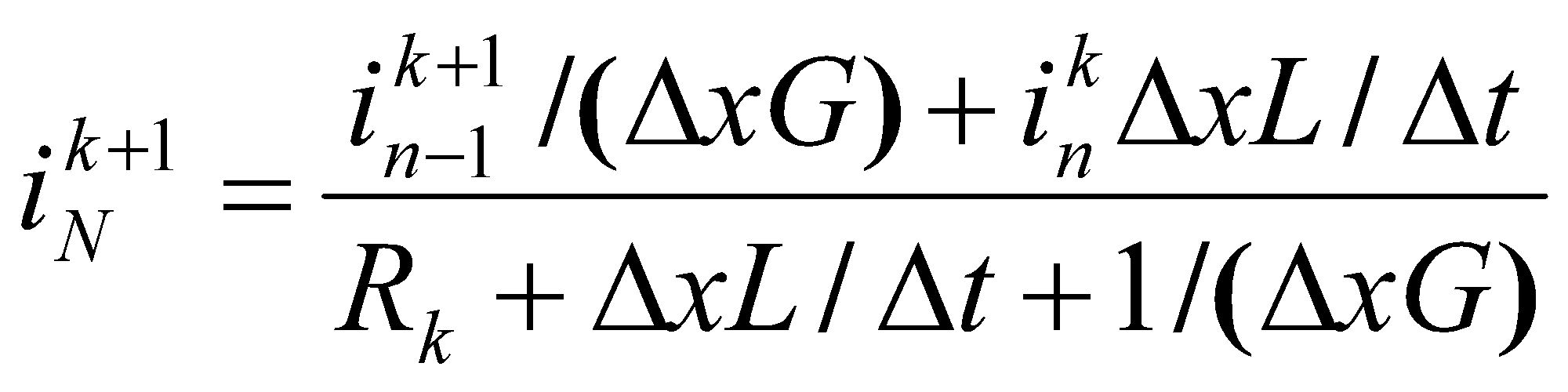
(21)

а ток в первом отрезке выражается через ток молнии I_М и сопротивление заземления начала коммуникации R_n

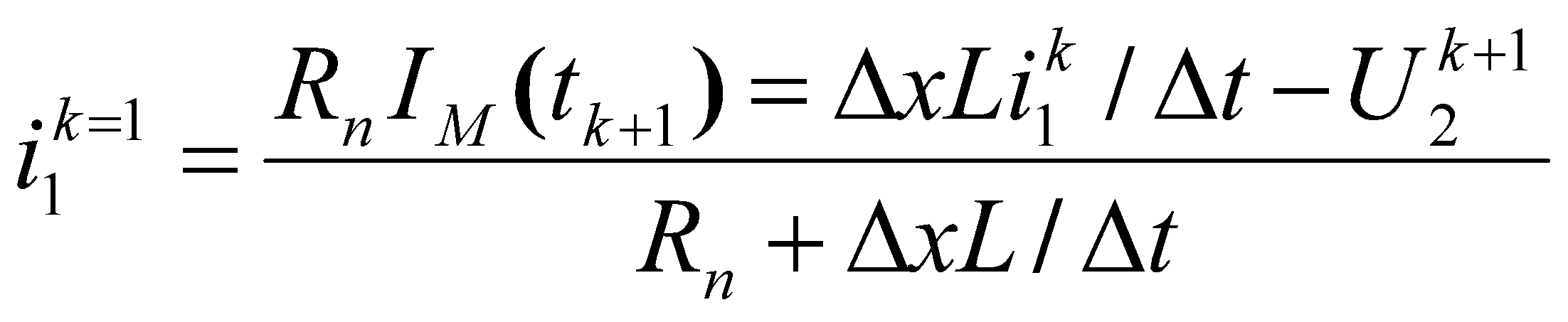
(22)

Обратная прогонка, необходимая для вычисления напряжений, кроме

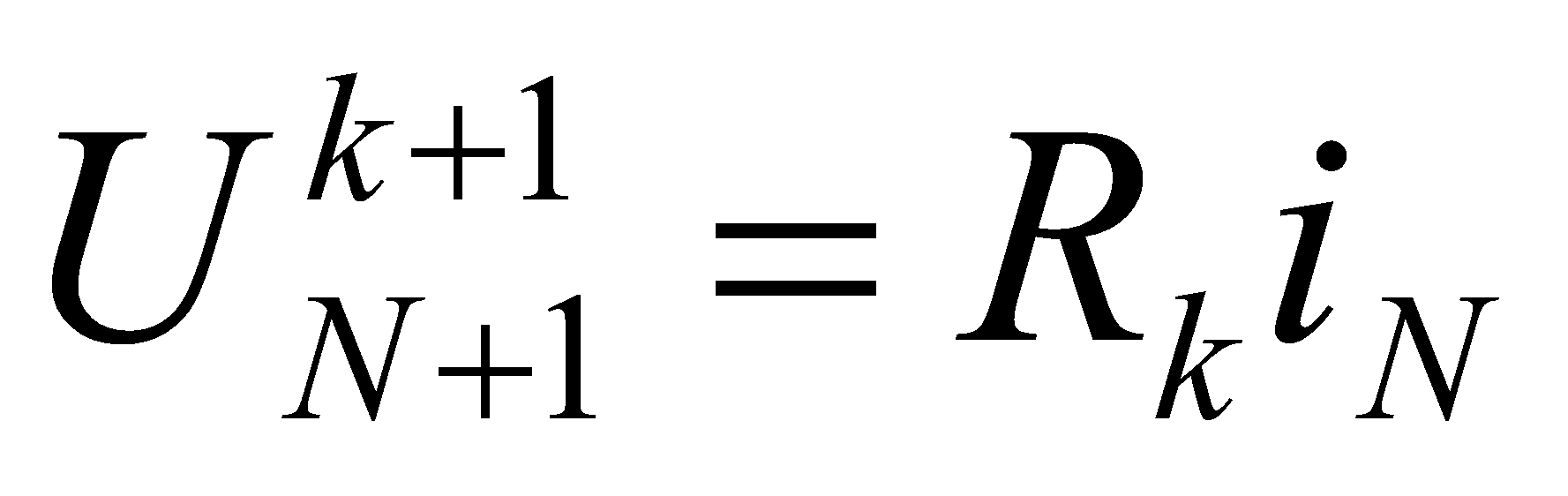
использует выражение

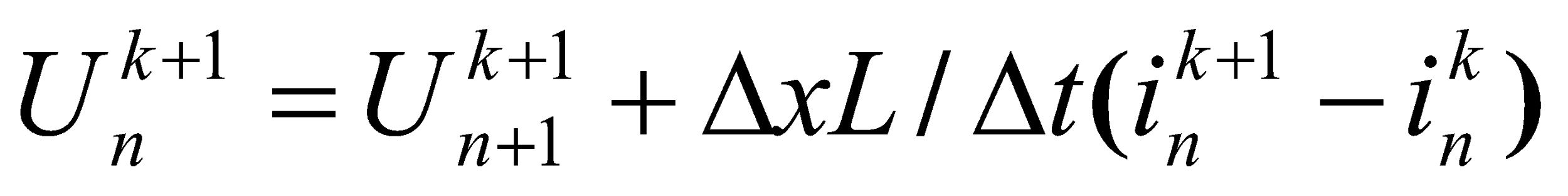
(23)

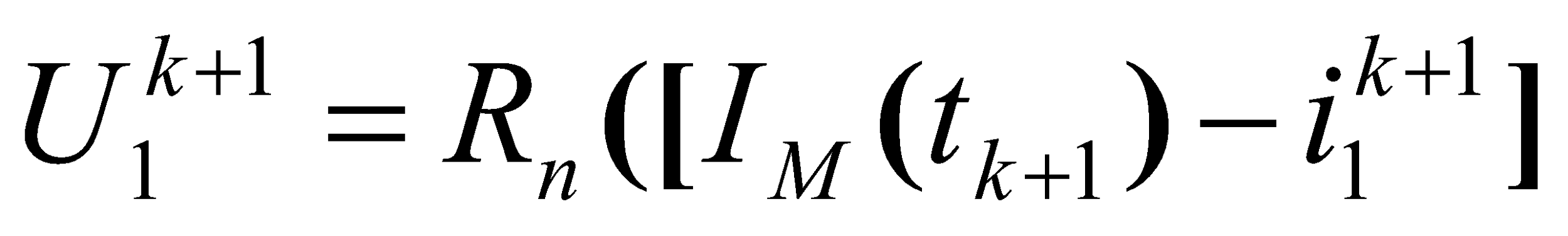
(24)

Алгоритм компьютерного расчёта принципиально не отличается от того, что был сформирован для ВЛ в разделе 3.

Первоначально надо знать размеры подземной коммуникации и вычислить для нее по формуле (17) сопротивление заземления при постоянном токе R_g. Оно необходимо, чтобы определить погонную проводимость утечки G =1/(lR_g). Длина и радиус коммуникации необходимы также для расчёта её погонной индуктивности (см. формулу (26) из следующего раздела). В качестве исходных данных потребуются еще сопротивления заземления на концах коммуникации.

Далее выполняются следующие операции:

Расчётный цикл повторяется для очередного момента времени, нарастающего с шагом ∆t вплоть до предельно заданного.

Точное решение, представленное на рис. 12, выполнено именно по этому алгоритму. Полезно заметить, что он пригоден при любых значениях сопротивлений заземления на концах коммуникации. Если положить их очень большими, например в 10⁶ Ом, режим растекания тока молнии с коммуникации будет определяться только её собственной проводимостью. Тогда делением напряжения в начале коммуникации (участок № 1) на ток молнии можно получить динамику изменения во времени сопротивления заземления протяженной заземляющей шины. Этот параметр очень важен для расчёта грозовых перенапряжений.

В заключение стоит заметить, что алгоритм пригоден для расчёта при любой форме импульса тока молнии. Для этого достаточно ввести в расчёт вместо формулы (9) соответствующее аналитическое выражение для I_М(t). Например, расчётные данные на рис. 13 характеризуют динамику изменения сопротивления заземления во времени для горизонтального проводника с параметрами, аналогичными использованным для рис. 12 . Предполагалось, что удельное сопротивление грунта равно 100 Ом м, а импульс тока молнии меняется во времени по биэкспоненциальному закону

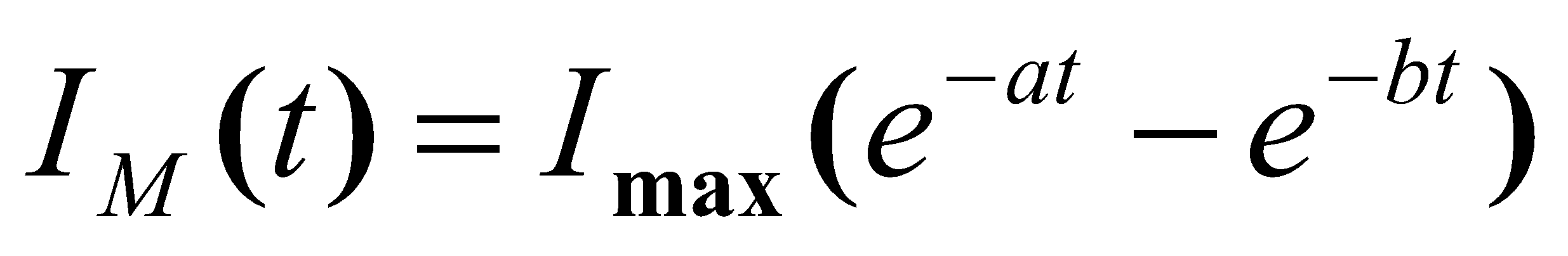
(25)

с временными константами a = 0,8 мкс^-1 и b = 0,007 мкс^-1 (примерно соответствует типичному импульсу тока первого компонента молнии с фронтом ~ 5 мкс и длительностью ~ 100 мкc).

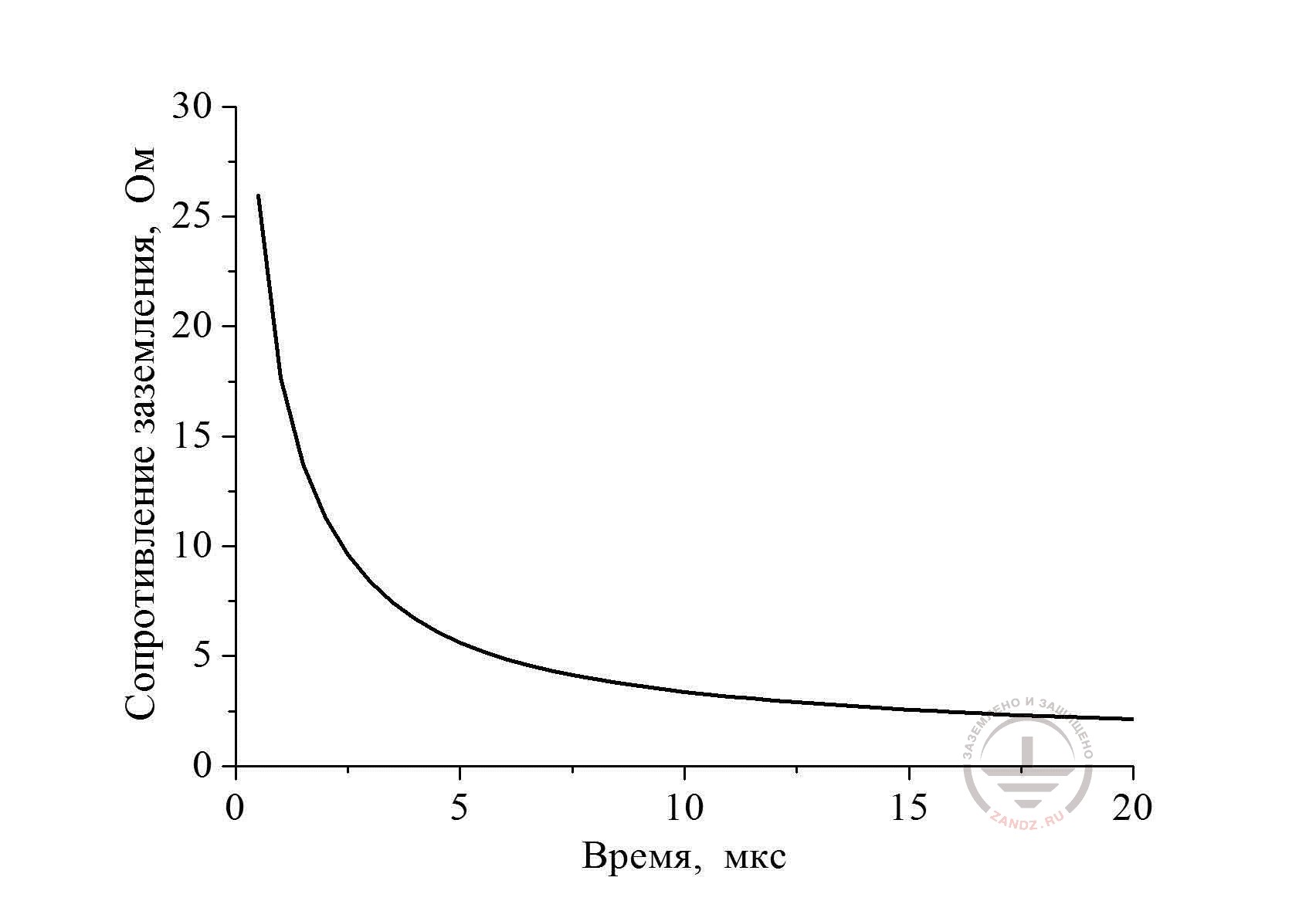
Динамика изменения во времени сопротивления заземления горизонтального трубопровода длиной 200 м и радиусом 5 см, который уложен в грунт с ρ =100 Ом м на глубину 0,5 м

Рис. 13. Динамика изменения во времени сопротивления заземления горизонтального трубопровода длиной 200 м и радиусом 5 см, который уложен в грунт с ρ =100 Ом м на глубину 0,5 м.

Потеря времени на расчёт не оказалась бесполезной, - можно видеть, что в течение первых 10 мкс сопротивление заземления проводника снизилось на порядок величины.

Э. М. Базелян, д.т.н., профессор
Энергетический институт имени Г.М. Кржижановского, г. Москва

Читайте далее "5. Полезные методические указания по расчёту токов нагрузки УЗИП"

Смотрите также:

Смотрите также: