Вторая часть статьи "Методика расчёта токов нагрузки УЗИП"
Решение задачи о разделении тока молнии между ВЛ, питающей поражённый объект, и его заземлителем, как уже было сказано выше, требует знания погонных значений индуктивности L и ёмкости С ВЛ, а также её погонного сопротивления R. Процесс описывается уравнениями в частных производных
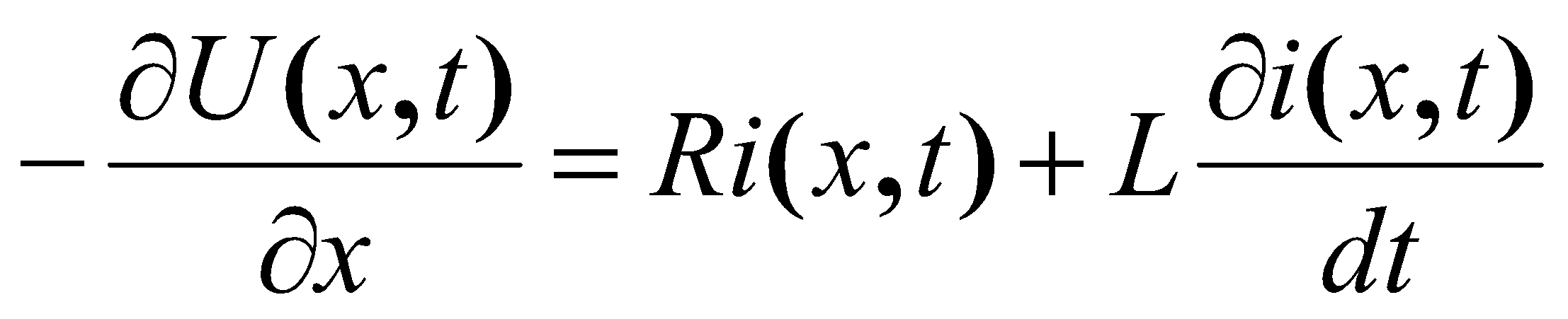
;
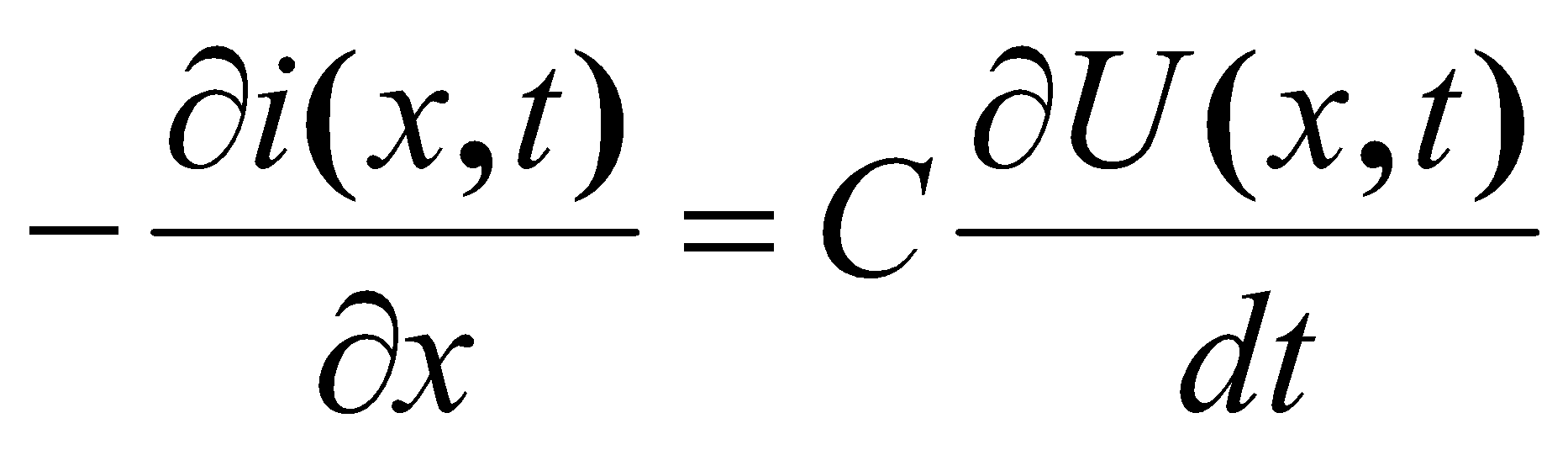
(1)
Они означают, что снижение напряжения на бесконечно малом участке длиной dx определяется падением напряжения от тока i на сопротивлении и на индуктивности (если конечно ток меняется во времени) этого участка, а уменьшение тока на том же участке в отсутствие поперечной проводимости определяется только током смещения через его ёмкость. Повторным дифференцированием уравнения легко привести к волновому более удобному для численного решения.
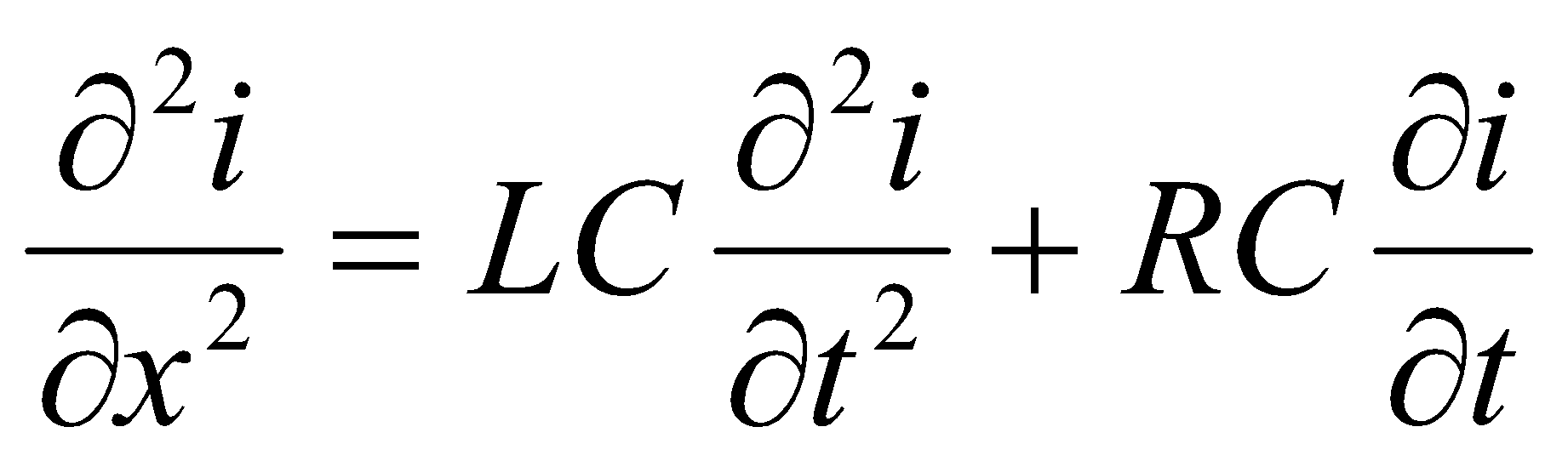 , (2)
, (2)
При этом частные производные представляются следующими разностными выражениями:
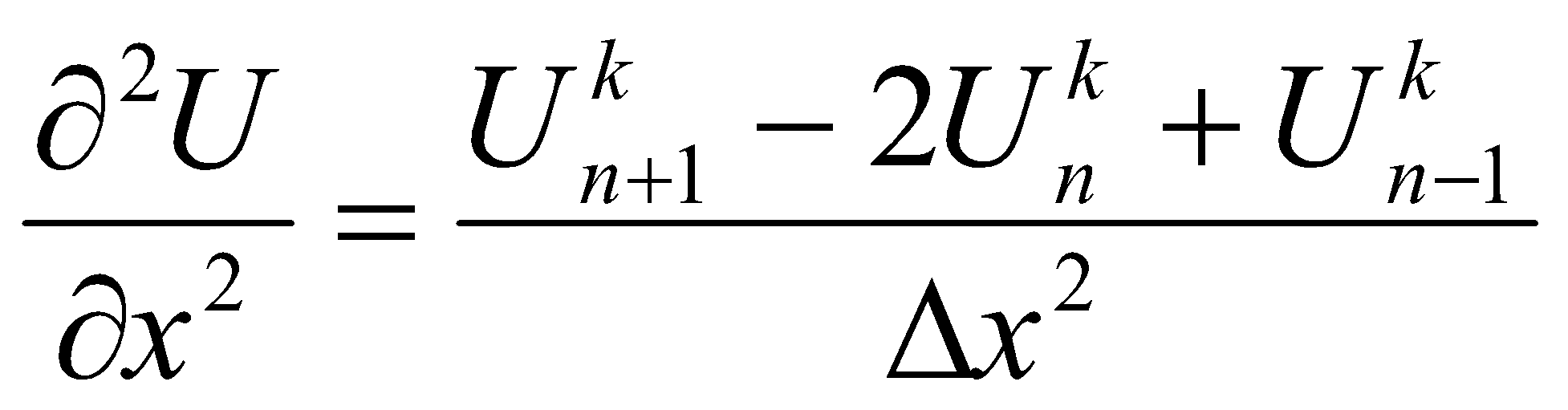
- для k-ой точки в n-ый момент времени
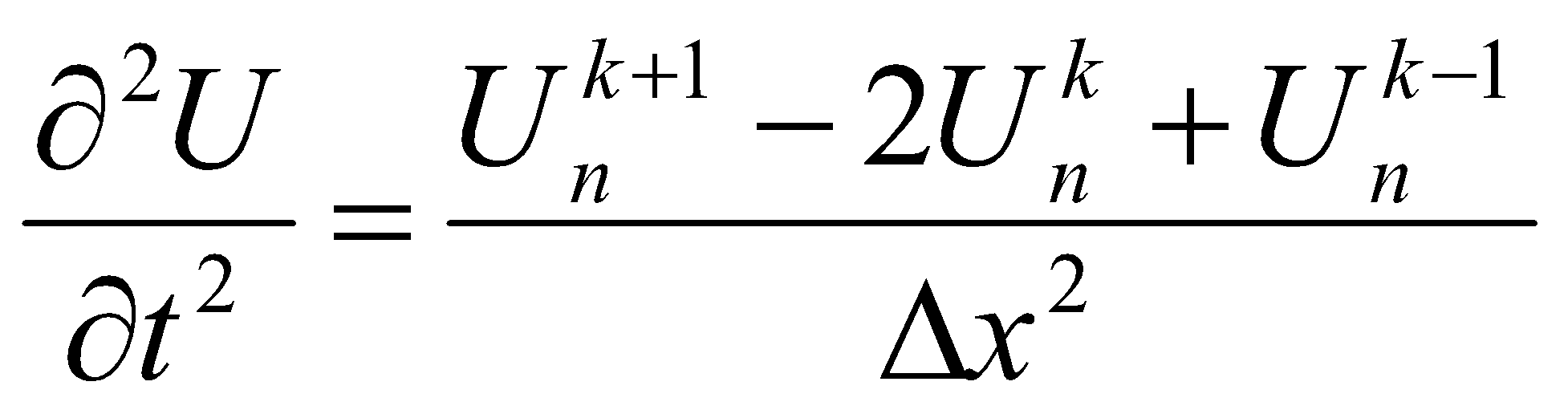
- для n-ного момента времени в k-ой точке,
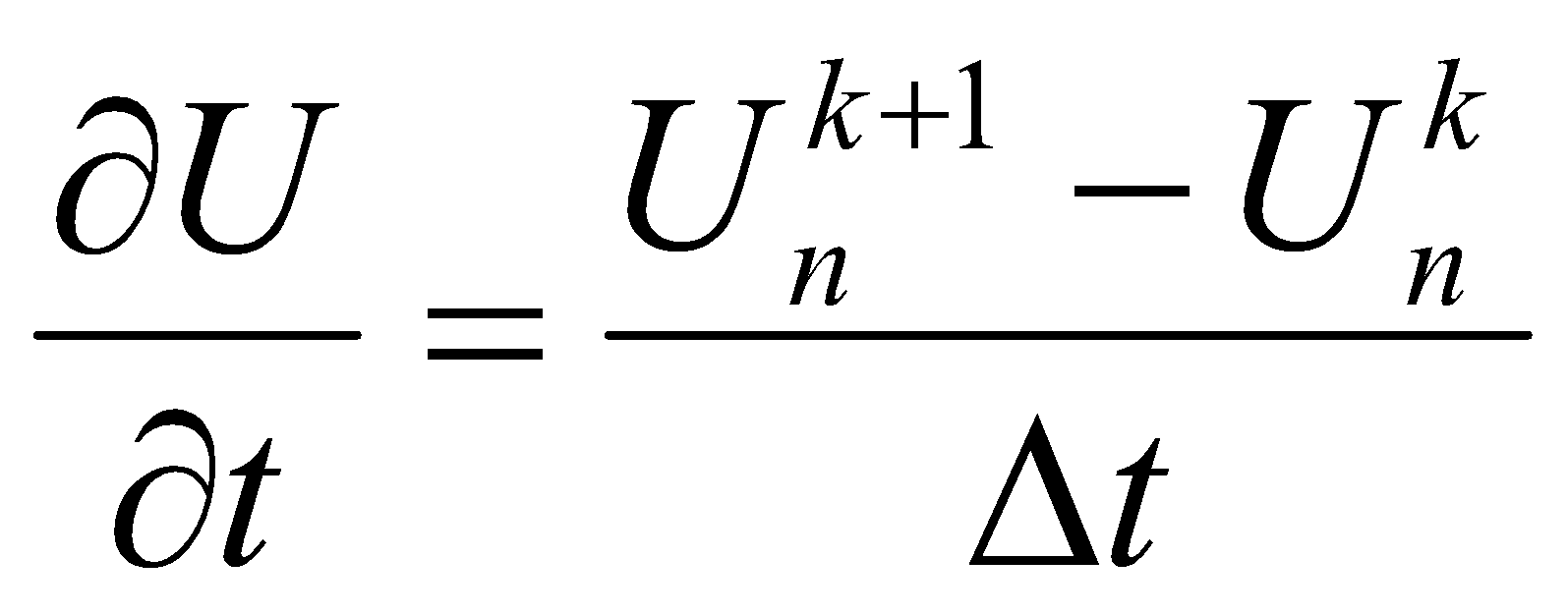
- для n-ного момента времени в k-ой точке.
Здесь Δx и Δt - расчётные шаги по длине линии и по времени соответственно. Производные для тока выглядят аналогично. С учётом выражений для производных уравнение для определения напряжений в расчётных узлах разностной схемы при прямой прогонке в направлении от пораженного объекта к ПС можно записать в виде
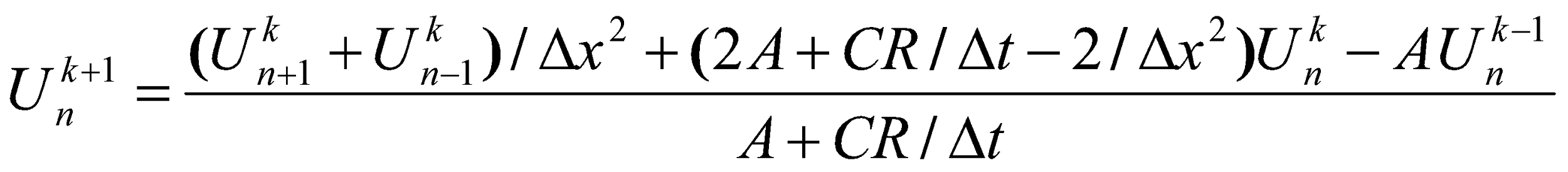
, (3)
где A = LC/Δt2, а запись Unk означает напряжение в момент времени tk в расчетной точке линии с координатой Xn.
Итак, чтобы найти напряжение в точке с координатой xn в очередной расчётный момент времени tk+1 нужно знать значения напряжения в этой точке для предыдущих моментов времени tk и tk-1, а также значения напряжения в точках с координатами xn-1 и xn+1 для момента времени tk. Если начальное (при t = 0) распределение напряжения по линии задано, а оно, как правило, равно нулю, то разностное выражение (3) позволяет последовательной прогонкой от начала ВЛ к ее концу вычислить напряжения всех расчетных интервалов, кроме первого и самого последнего. Для их определения требуется привлечь граничные условия, которые описывают схему питания в начале линии и нагрузку на её конце. Например, при пробое изоляции проводов грозовым перенапряжением концы проводов ВЛ оказываются присоединенными к заземлителям защищаемого объекта и питающей подстанции. Тогда на подстанционном конце, которому соответствует схема замещения рис. 2, напряжение последнего узла определяется через ток в сопротивлении заземления ПС RP
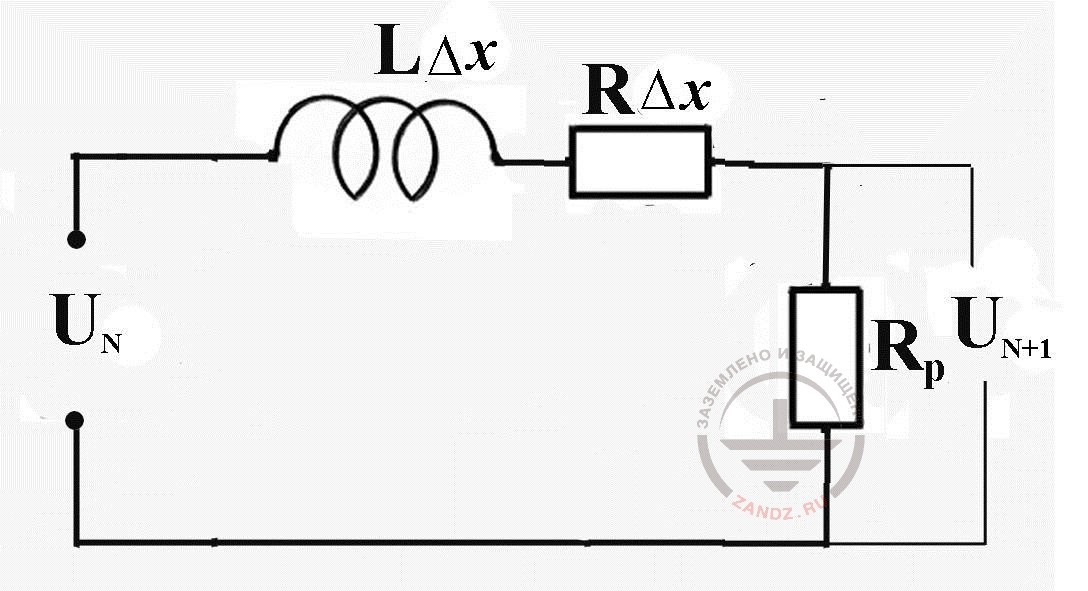
Рис. 2. Схема замещения для расчета напряжения последнего узла схемы и тока в заземлителе ПС RP
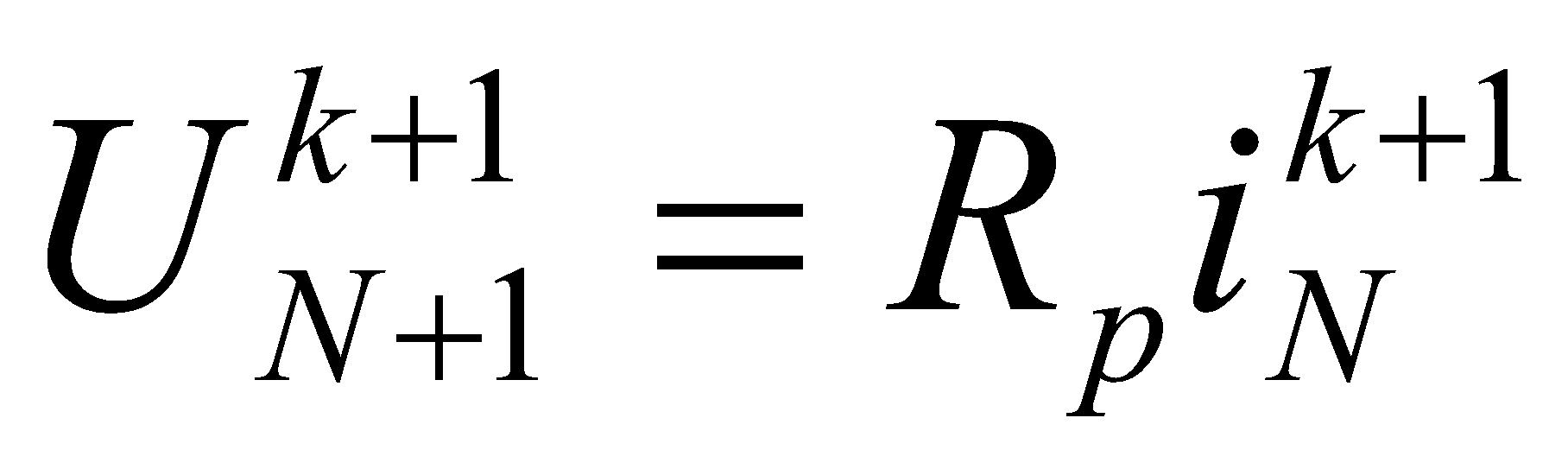
, где
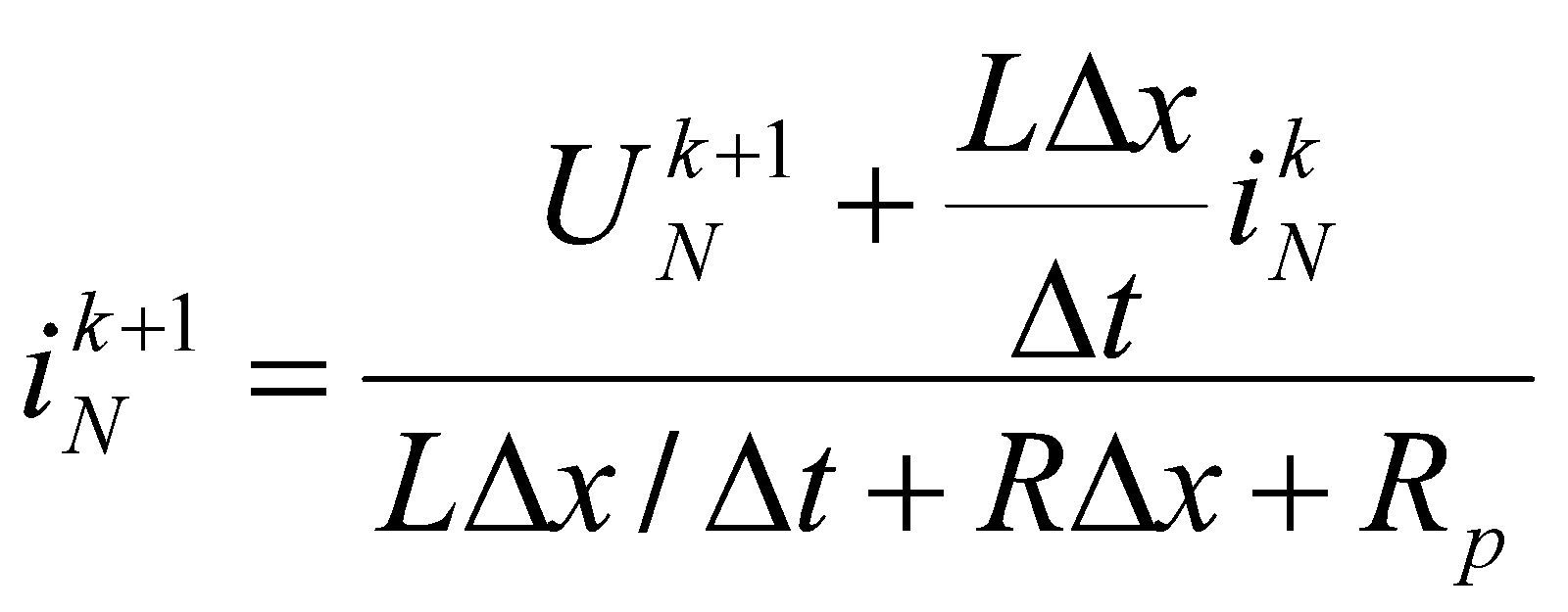
(4)
Здесь N – полное число пространственных отрезков ВЛ длиной по ∆x, а вторая расчётная формула в (4) получена переводом линейного дифференциального уравнения для напряжения на контуре
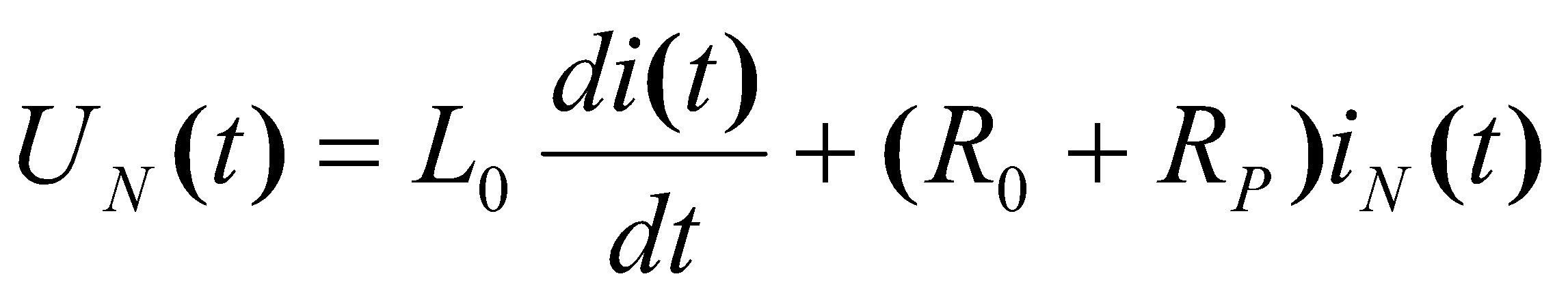
(5)
в разностную форму, причём величина ink - ранее найденный ток для момента времени tk, а значения L0 = ∆xL и R0 = ∆xR – индуктивность и сопротивление расчётного отрезка ∆x.
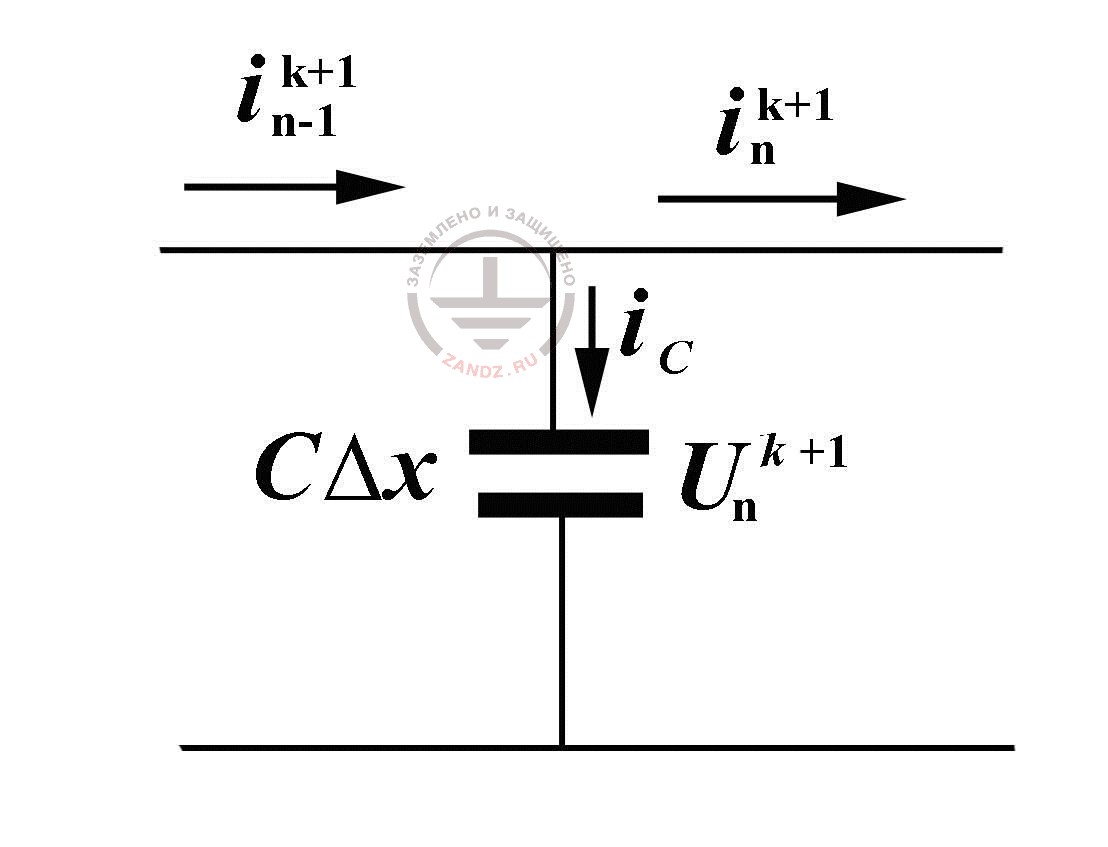
Рис. 3. К расчету токов в отрезках ВЛ при обратной прогонке
Теперь, когда известно значение тока в конце линии для очередного момента времени tk+1 и известны все значения напряжений в узлах схемы, обратной прогонкой, двигаясь от конца ВЛ к ее началу, можно определить токи во всех отрезках, руководствуясь элементарной схемой замещения рис. 3. Как можно видеть, ток вдоль линии меняется за счёт ёмкостного тока iC, благодаря которому изменяется заряд и напряжение на ёмкости расчётного отрезка. Поэтому
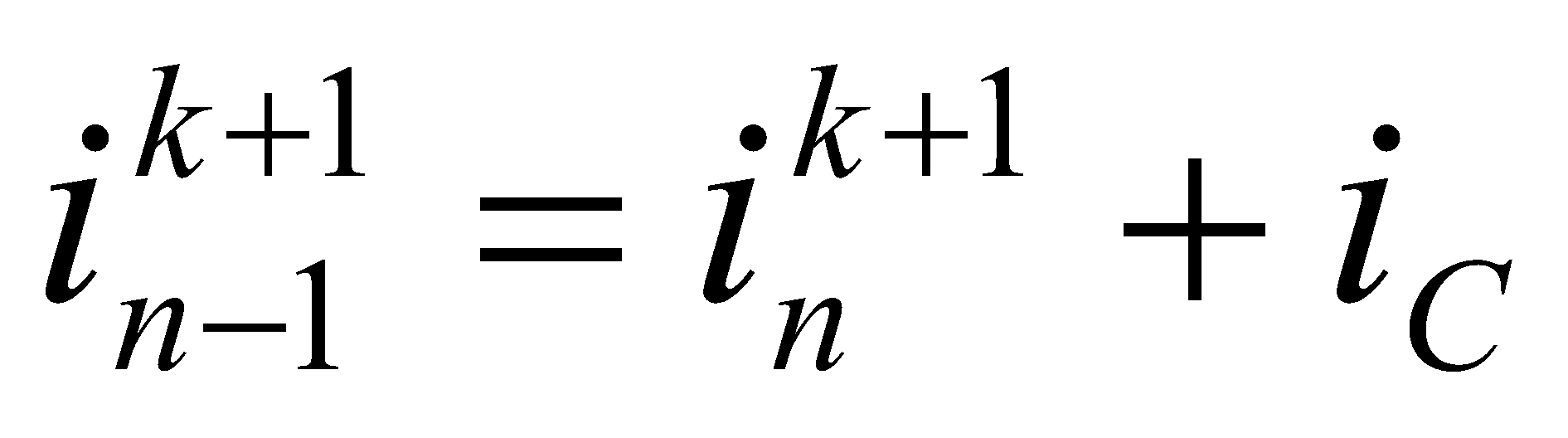
(6)
где
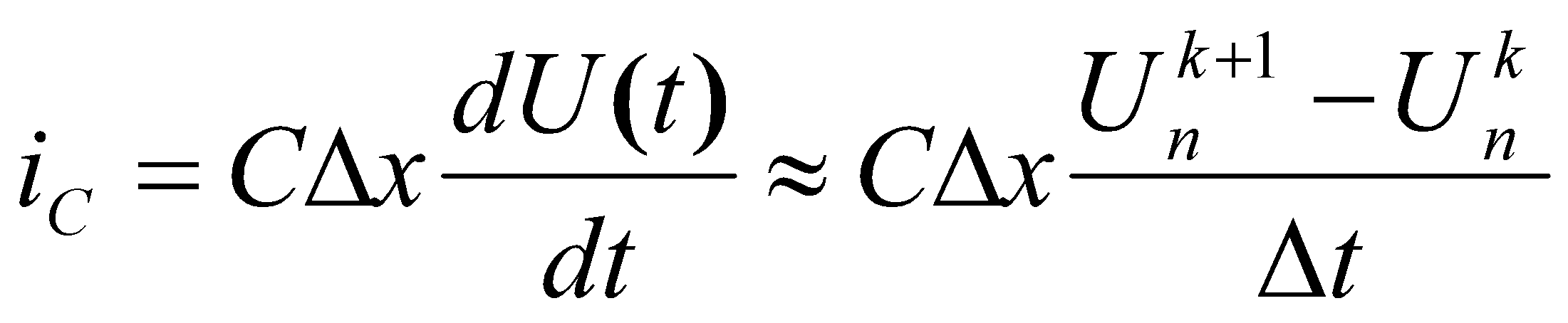
(7)
Дополнительного внимания требует только первый узел расчётной схемы, где фигурирует ток молнии и сопротивление заземления поражённого объекта. Схема замещения для этого узла (рис. 4) позволяет наконец завершить расчётный цикл, выразив пока ещё неизвестное напряжение U1k=1 через текущее значение тока молнии Iм(tr+1) и уже вычисленный ток i1k+1
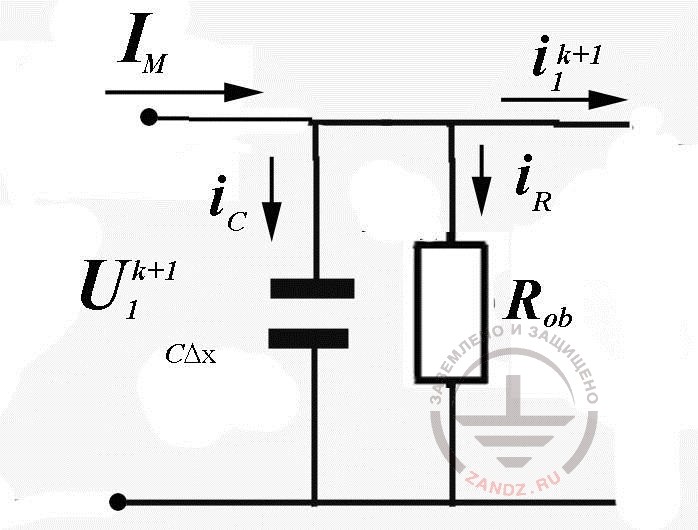
Рис. 4. Схема замещения узла № 1 расчетной схемы.
Здесь i1k+1+iR+iC=IМ, что по аналогии с проведёнными выше вычислениями даёт
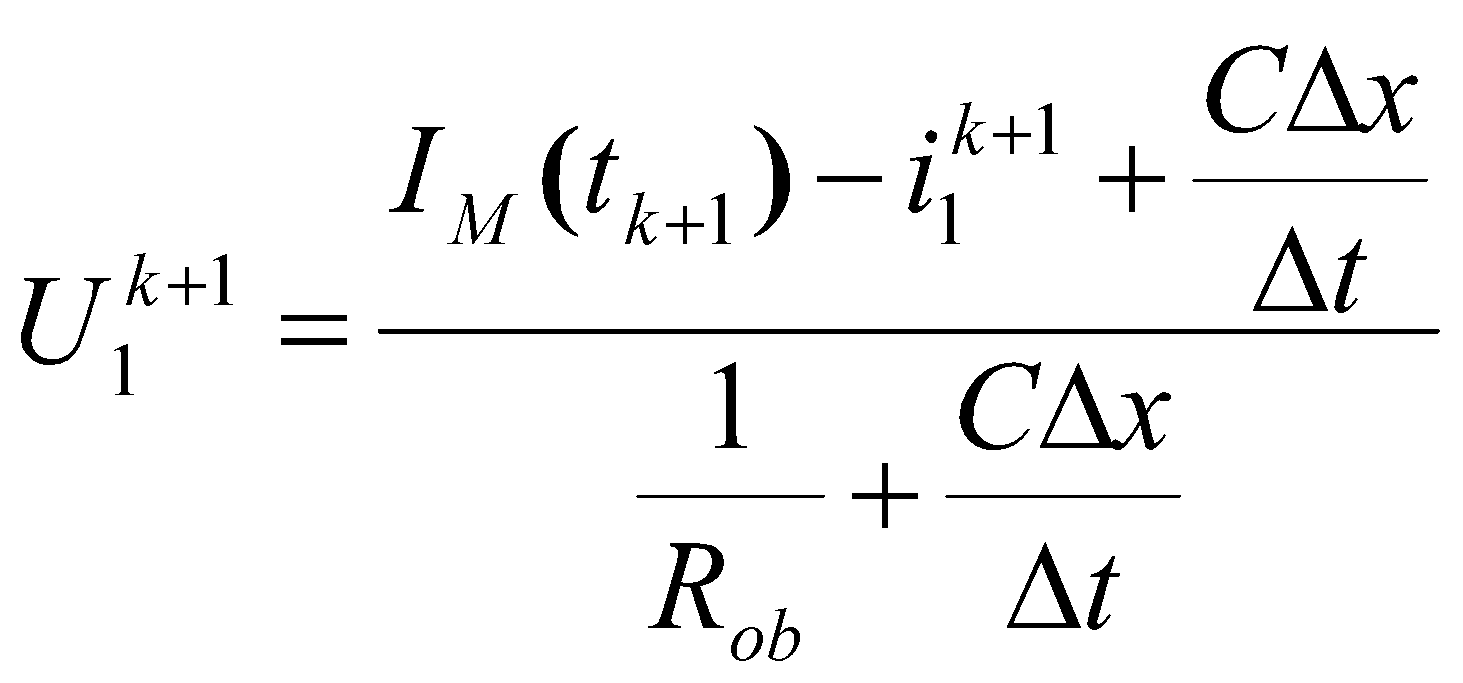
(8)
Все значения искомых параметров для расчётного момента времени tk+1 найдены. Можно переходить к следующему временному шагу и т.д., пока не будет достигнут нужный момент времени.
Изложенный алгоритм может быть покажется неоправданно длинным, но сложности в нём нет никакой. И прямая прогонка, нужная для определения напряжений узлов расчётной схемы, и обратная прогонка для вычисления токов расчётных отрезкой ВЛ практически никогда не меняется. Исключение составляет только расчёт протяженных заземляющих шин, где приходится дополнительно учитывать проводимость утечки тока в грунт (вопрос будет рассмотрен ниже). Изменения касаются только условий на концах линии, где нужно вычислять токи в обычной схеме замещения с сосредоточенными параметрами – задача вполне привычная для инженера-электрика.
На рис. 5 и 6 для примера представлены результаты численного решения рассмотренной выше задачи.
Математическое выражение для тока молнии заимствовано из стандарта МЭК и из отечественной инструкции СО-153-34.21.122-2003.
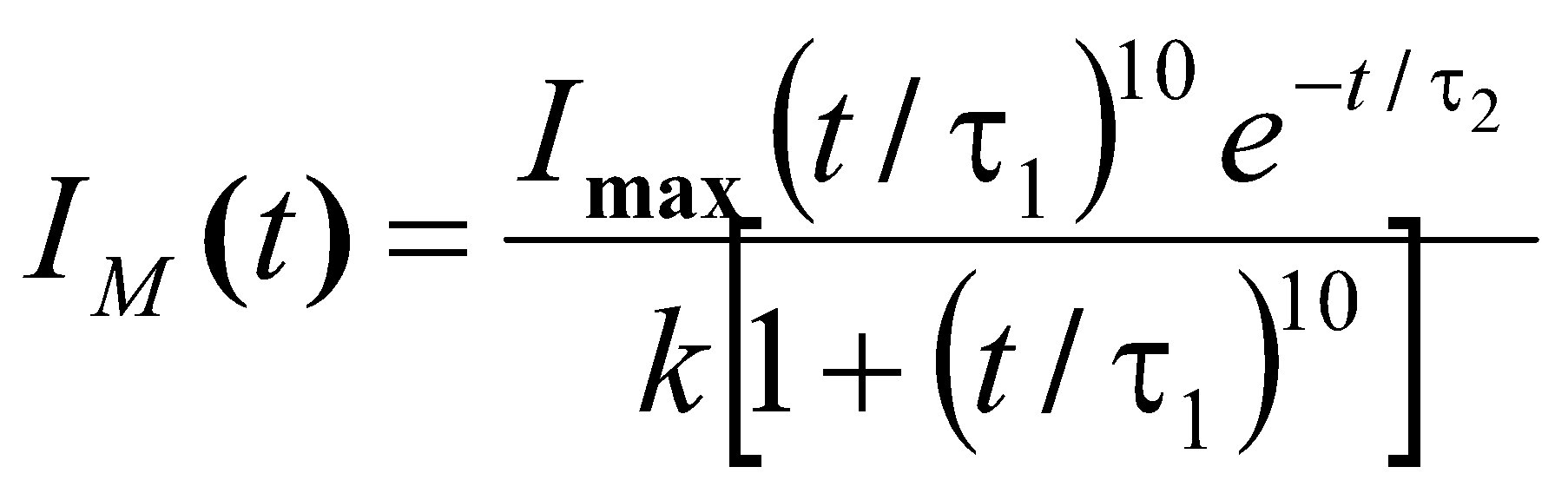
(9)
Стоит заметить, что оно крайне неудобно для аналитики и численных расчётов, особенно если исходные параметры k, τ1 и τ2 выбраны для описания типового импульса 10/350 мкс.
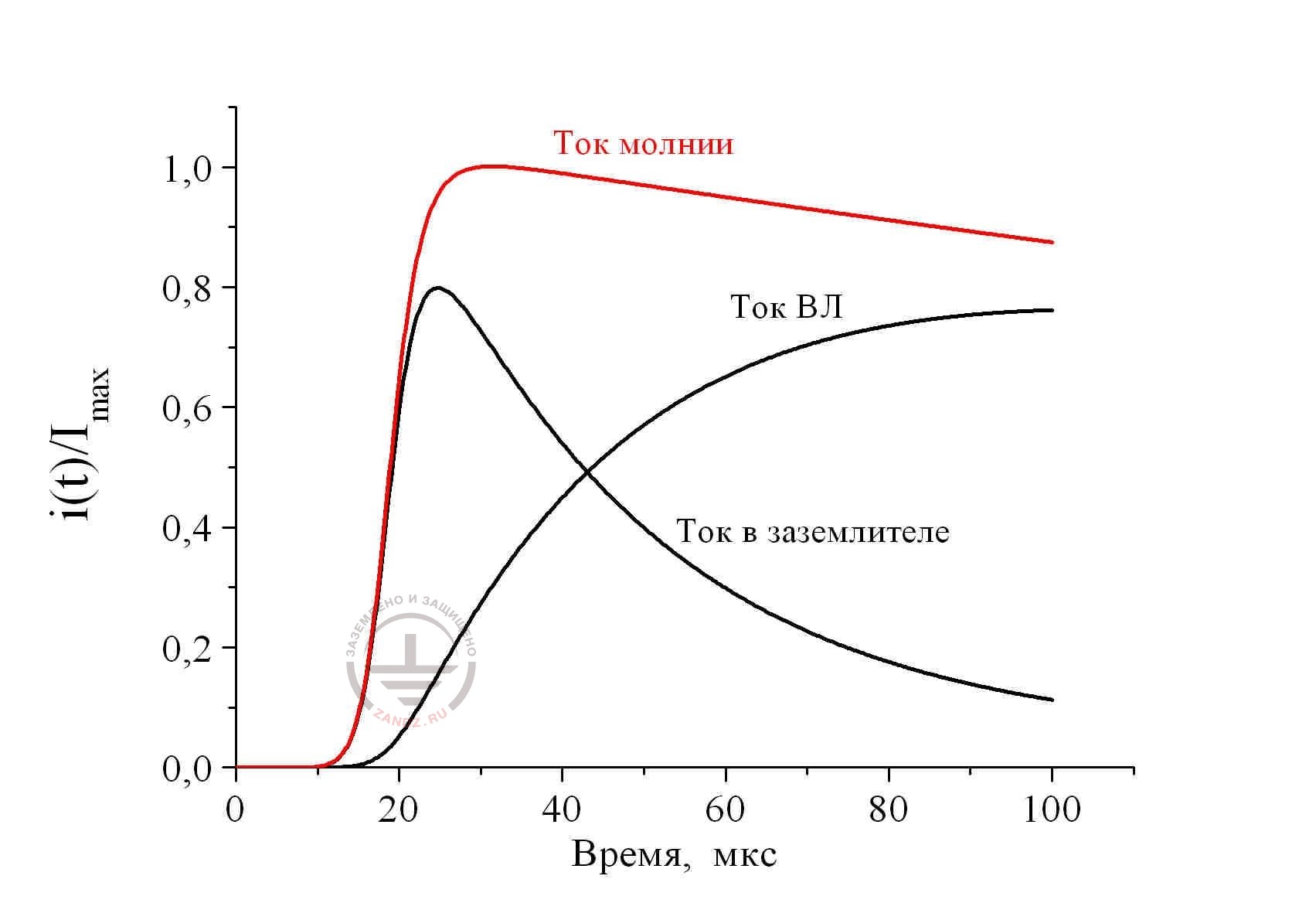
Рис. 5. Распределение тока молнии 10/350 мкс между металлическими коммуникациями пораженного объекта с сопротивлением заземления 10 Ом; длина ВЛ 300 м: сопротивление заземления ПС 1 Ом.
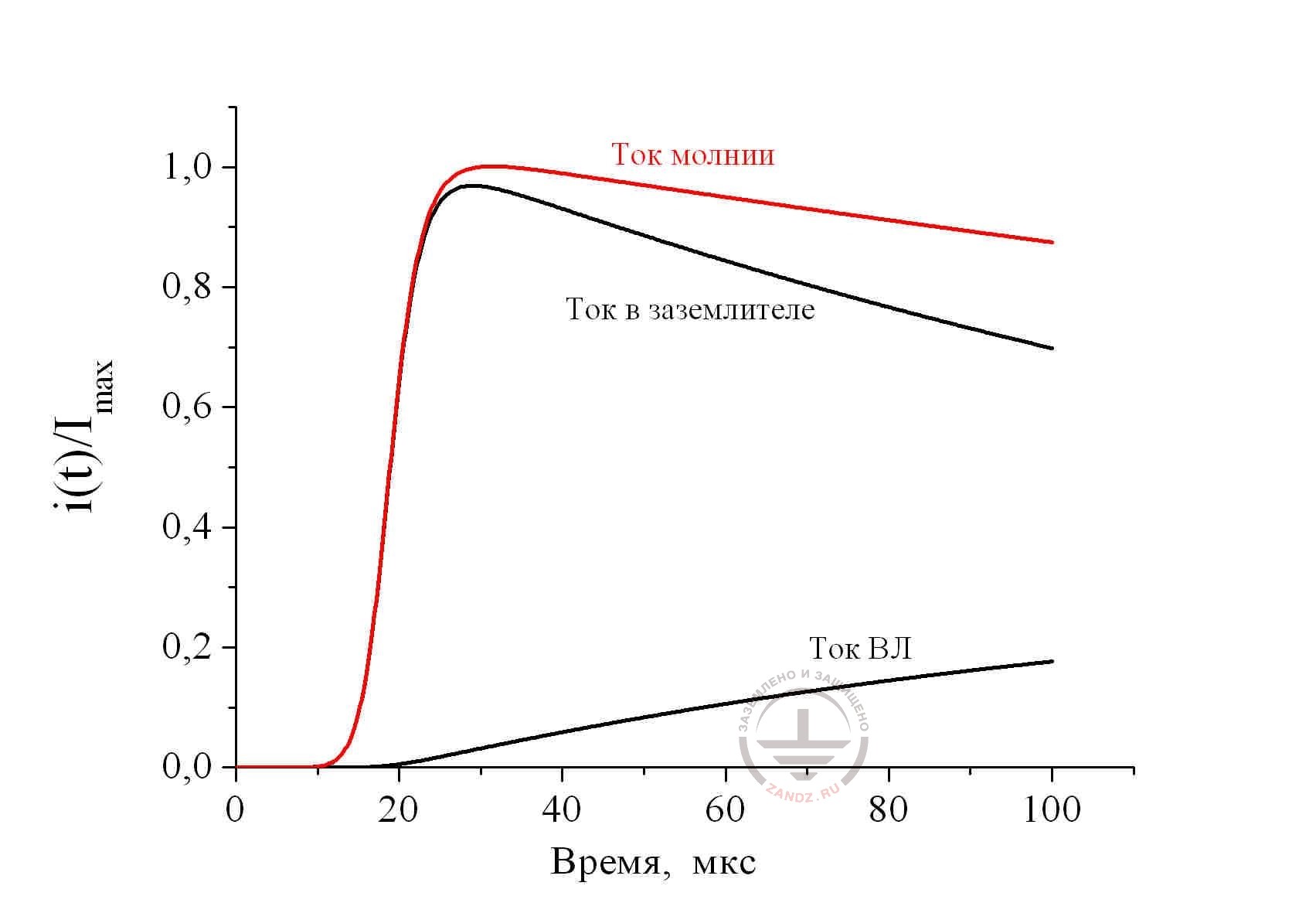
Рис. 6. Распределение тока молнии 10/350 мкс между металлическими коммуникациями пораженного объекта с сопротивлением заземления 1 Ом; длина ВЛ 300 м: сопротивление заземления ПС 1 Ом.
Представленные решения выполнены для участка ВЛ длиной 300 м. Сопротивление заземления поражённого объекта принято равным 10 Ом для рис. 5 и 1 Ом для рис. 6; сопротивления заземления на ПС равнялось 1 Ом. Легко убедиться, что полученные результаты имеют очень мало общего с фирменными предписаниями рис. 1, где ток в заземлителе пораженного объекта при любых обстоятельствах рекомендуется принимать равным 50% от тока молнии. В действительности его доля может очень существенно меняться во времени (условия расчета для рис. 5), а амплитудное значение может едва ли не совпадать с током молнии (условия расчёта на рис. 6). Соответственно не остается постоянной и доля тока, ответвляющегося в ВЛ через сработавшие УЗИП. Временные параметры импульса, который их нагружает, очень мало похожи на стандартизованный импульс тока молнии. Уже только одно это обстоятельство делает необходимым численный расчёт. Без него невозможно оценить энерговклад в УЗИП, а значит и выбрать конкретный тип защитного устройства.
Решения, которые здесь представлены, выполнены с временным шагом 1 нс. Таким образом, расчётный интервал в 100 мкс был разбит на 105 временных шагов. Пространственный шаг принят равным 1 м. Следовательно, потребовалось выполнить 3×107 расчетных циклов. Тем не менее, расчет продолжался меньше 1 минуты. Как видите, не стоит пренебрегать компьютером!
Закономерен вопрос об учете параметров УЗИП в расчёте. Легко убедиться, что им не нашлось места в расчётных схемах. Это закономерно, потому что собственное сопротивление сработавшего УЗИП мало по сравнению с сопротивлением заземления объекта или ПС и практически не сказывается на величине тока.
Итак, никакие универсальные схемы с раз и навсегда записанными процентными долями тока молнии к верным представлениям о токовой нагрузке УЗИП привести не могут. Нужно грамотное конкретное решение и главный вопрос заключается в том, чтобы по возможности избежать в нем громоздких вычислений, тем более, далеко не всегда оправданных.
Э. М. Базелян, д.т.н., профессор
Энергетический институт имени Г.М. Кржижановского, г. Москва
Читайте далее "3. Использование схемы замещения с сосредоточенными параметрами при прямом ударе молнии в объект или в питающую его ВЛ"
Смотрите также:
- Видеозапись и стенограмма вебинара с профессором Э. М, Базеляном “Для чего нужны УЗИПы”
- Принципы подбора ограничителей перенапряжений в низковольтных электрических сетях на примере устройств Leutron
- Бесплатные вебинары для проектировщиков заземления и молниезащиты
- Проекты по заземлению и молниезащите в форматах dwg, pdf
- Бесплатные консультации и помощь в расчётах заземления и молниезащиты
Смотрите также:
 Молниезащита жилых и общественных зданий - ответы на частые вопросы при проектировании
Молниезащита жилых и общественных зданий - ответы на частые вопросы при проектировании
 Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 1
Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 1
 Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 2
Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 2
 Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 3
Вебинар "Молниезащита больших территорий: парки, площадки, территории заводов." Страница 3

