Из цикла статей "Заземление в молниезащите - ответы на частые вопросы при проектировании".
Это полагается делать в процессе завершения монтажных работ и перед каждым грозовым сезоном. Принцип работы любого измерительного прибора сводится к методу амперметра и вольтметра. Встроенный генератор прибора нагружает контролируемый заземлитель током известной величины I, а вольтметр измеряет напряжение на заземлителе UЗ относительно бесконечно удаленной точки. По закону Ома частное от деления этих величин дает сопротивление заземления. RЗ = UЗ/I. Проблема организации измерений связана только с монтажом схемы. Для ввода тока надо поместить в грунт вспомогательный токовый электрод, а для измерения напряжения следует найти "бесконечно далекую" точку нулевого потенциала, чтобы ввести в неё ещё один вспомогательный электрод для подключения вольтметра. Всё это требует немалого свободного пространства. Иначе никак не исключить взаимного влияния между электродами и искажений ими режима растекания тока. Вот как рекомендуется размещать элементы измерительной цепи в существующих руководствах (рис. 10).
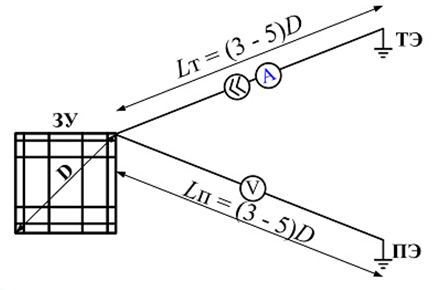
Рисунок 10
Здесь все опять определяется максимальным габаритным размером заземляющего устройства. Чем он больше, тем медленнее снижается потенциал в грунте при растекании тока. До нуля он снизится в бесконечности и туда с измерительными проводами не добраться. Приходится соглашаться на некоторую ошибку, скажем, в пределах 10% (для молниезащитных дел вполне приличная точность). Расчетные зависимости на рис. 11 и 12 показывают, как снижается потенциал на поверхности земли в окрестности протяженной горизонтальной шины радиусом 10 мм и в окрестности контура заземления с ячейками 10х10 м из таких же шин. В первом случае для требуемого снижения потенциала надо удалиться от заземлителя примерно на длину шины, во втором – на две диагонали контура. Это могут быть совсем не малые расстояния, потому что контур заземления с диагональю в 200 м и более в технике не редкость. Тем не менее, в руководствах рекомендуются ещё более значительные расстояния. Они необходимы, чтобы устранить мешающее влияние вспомогательного электрода, через который замыкается ток нагрузки заземлителя.
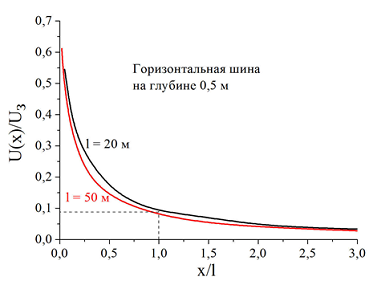 Рисунок 11
Рисунок 11
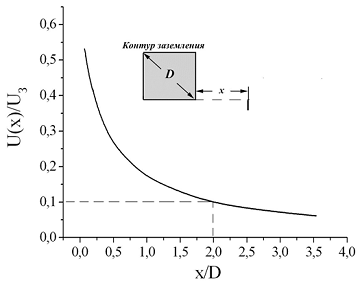 Рисунок 12
Рисунок 12
Коррекция методической погрешности измерений
В статье уже упоминалось о полной аналогии полей электрических зарядов и постоянного тока. Если расположить на каком-то расстоянии электрические точечные заряды противоположного знака, на прямой между ними всегда найдется точка нулевого потенциала, потому что разнополярные заряды создают различные по знаку потенциалы. Электроды с током в земле подобны таким зарядам. С одного электрода ток стекает в землю (пусть он будет условно положительным), а у другого собирается из земли (электрод с отрицательным током). Может не стоит уходить в бесконечность, а поискать точку нулевого потенциала на прямой между электродами? Так родилась более компактная схема с расположением всех электродов на одной прямой (рис. 13)

Рисунок 13
Если электроды действительно точечные (или, как показано на рисунке, полусферические) точку нулевого потенциала нечего искать – в силу симметрии она будет расположена точно по середине между электродами. Но оказывается, что для точного измерения сопротивления заземления потенциальный электрод надо погрузить в грунт не в ней, а совсем в другом месте. Теперь для доказательства не избежать вычислений, хотя и предельно простых.
Аналогия с уравнениями электростатики ставит формальное тождество между электрическим зарядом q и током I, а аналогом диэлектрической проницаемости ε становится проводимость грунта γ =1/ρ. При такой аналогии напряжение на уединенной полусфере радиуса r0 относительно точки нулевого потенциала равно
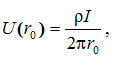
что приводит к известному выражению для сопротивления заземления полусферы в однородном грунте
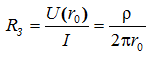
Во время измерений на обозримом расстоянии друг от друга rtok находятся два электрода с токами различного направления I и –I. Теперь должен быть принят во внимание принцип наложения, по которому в линейной среде потенциал любой точки определяется как сумма потенциалов от всех существующих источников и потому измеренное напряжение окажется меньше
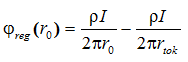
Второе слагаемое в этой формуле определяет ошибку, занижающую величину измеренного сопротивления по отношению к истинному значению на величину
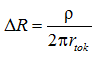
Чтобы скомпенсировать эту ошибку, измерение напряжения на заземлителе надо производить не относительно точки нулевого потенциала, а относительно некоторой точки на расстоянии rpot, где потенциал φ(rpot) отрицательный, вследствие чего измеренное напряжение Ureg = φreg(r0) - φ(rpot) увеличится.
Естественно, что потенциал в точке rpot также определяется двумя токами:
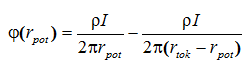
Ошибки в измерениях не будет в случае выполнения равенства
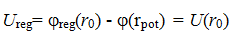
Предлагаю читателю подставить в последнюю формулу все найденные значения, сделать приведение подобных членов и, получив в итоге выражение
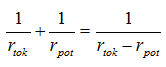
разрешить его относительно искомого расстояния rpot, куда надо устанавливать потенциальный электрод. У тех, кто не забыл школьную алгебру, получится
Рекомендации в отечественных нормативных документах
Соблазнительная рекомендация, не задумываясь, устанавливать потенциальный электрод на расстоянии 0,62rtok от измеряемого заземлителя любой конструкции в России не прижилась. Отечественные специалисты не увидели каких-либо весомых оснований для распространения частного вывода на заземлитель любой конструкции. Но сама методика размещения всех электродов на одной прямой фактически узаконена (РД 153-34.0-20-525-00). Расстояние от заземлителя до вспомогательного токового электрода рекомендуется выбирать из условия rtok ≥ 3D, где D – максимальный габаритный размер заземляющего устройства. Потенциальный электрод последовательно, с шагом ∆d = 0,1rtok размещают на прямой, соединяющей заземлитель с токовым электродом и измеряют либо напряжение между заземлителем и потенциальным электродом, либо сразу сопротивление заземления (если прибор градуирован в омах). Далее строится зависимость измеренных значений от положения потенциального электрода (рис. 14). Если измерения в точках rpot = 0,4rtok и rpot = 0,6rtok отличаются в пределах 10%, принимается, что истинное значение сопротивления заземления соответствует расположению потенциального электрода в точке rpot = 0,5rtok.
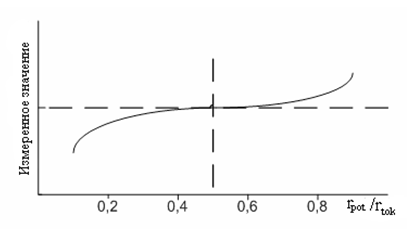
Рисунок 14
Методика заметно усложняется, когда кривая на рис. 14 не имеет явно выраженного плоского участка. Тогда рекомендованные измерения и построение графика следует повторить для rtok = 2D. Далее принимается, что точка пересечения построенных кривых (в относительных координатах rpot/rtok на оси абсцисс) определяет "правильное" место установки потенциального электрода.
Рекомендованная процедура построения не вызывает особых проблем для одиночных горизонтальных шин или вертикальных стержневых электродов. Измерения здесь дают картину, очень похожую на рис. 14, условие с 10%-ным расхождением результатов в точках rpot = 0,4rtok и rpot = 0,6rtok обычно выполняется и потому удается четко определить точку нулевого потенциала. К тому же одиночные горизонтальные электроды, а тем более вертикальные, редко бывают особо большой длины, что позволяет выполнить условие rtok ≥ 3D. Ситуация для контуров заземления большой площади заметно сложнее. Их диагональ вполне может превысить 200 – 300 м. Найти свободное почти километровое пространство в районе городской или промышленной застройки можно считать исключительно большим везением. К тому же контур заземления даже не слишком больших размеров перестает вписываться в требования методических указаний.
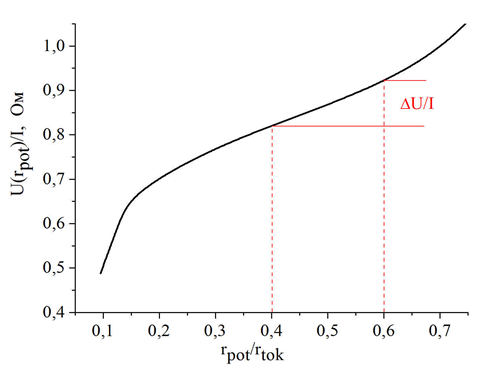
Рисунок 15
На рис. 15 компьютерное моделирование воспроизводит результаты для контура заземления, в роли которого выступает ленточный железобетонный фундамент здания площадью 50 х 50 м2. Фундамент заглублен в грунт на 3 м. Легко убедиться, что значения напряжения относительно точек rpot = 0,4rtok и rpot = 0,6rtok отличаются больше, чем на предписанные 10%. К тому же построенная кривая не имеет явно выраженного горизонтального участка. Если следовать "Методическим указаниям", здесь потребовалась бы еще одна серия измерений при rtok = 2D.
Полезно помнить, что любые Методические указания носят рекомендательный характер. Есть смысл разобраться в таких рекомендациях. А начинать удобнее с подхода к определению точки нулевого потенциала. На построенной кривой она совпадает с точкой перегиба и определяется экстремумом первой производной. Не надо пугаться слегка позабытых слов. Ничего сложного делать не придется. Значения напряжения между заземлителем и потенциальным электродом при его перемещении с шагом ∆r = 0,1rpot уже измерены. Достаточно из каждого очередного измеренного значения, например Uk, вычесть предыдущее измерение Uk-1 и отложить полученную величину ∆U = Uk – Uk-1 на графике для значения на оси абсцисс, отвечающего середине интервала, на котором стояли потенциальные электроды. Полученные таким образом точки опишут характерную кривую с минимумом. Положение минимума – это и есть точка нулевого потенциала (рис. 16).
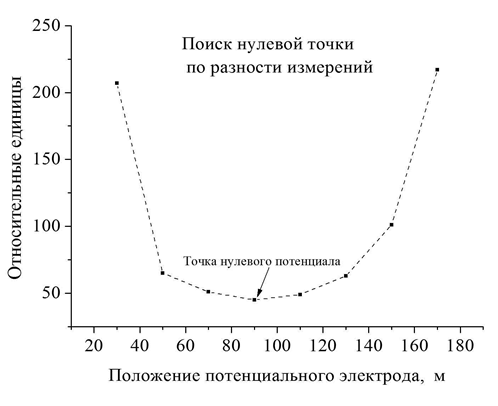
Рисунок 16
Можно поступить ещё проще. Сразу измерять напряжение между парой потенциальных электродов, размещенных на расстоянии ∆r = 0,1rpot друг от друга, последовательно смещаясь по прямой от изменяемого заземлителя к вспомогательному токовому электроду. Минимальное из этих значений определит положение точки нулевого потенциала. Она будет находиться примерно по середине между потенциальными электродами в "минимальном" измерении. Необязательно даже выбирать шаг смещения потенциальных электродов равным ∆r = 0,1rpot. Важно, чтобы он был одинаковым.
Теперь, когда с точкой нулевого потенциала ясно, полезно осознать, нужна ли она для определения сопротивления заземления. Пожалуйста, не удивляйтесь возникшему вопросу. Относительно точки нулевого потенциала измеряется напряжение, задающее после деления на ток величину сопротивления заземления. Из всего сказанного выше явствует, что присутствие токового электрода за счет своего электрического поля снижает потенциал контролируемого заземлителя. В итоге измеренное сопротивление оказывается ниже (в определенных условиях заметно ниже) своего фактического значения. Вспомните, именно для компенсации методической ошибки подобного рода возникла рекомендация располагать потенциальный электрод не в точке нулевого потенциала, а на расстоянии rpot = 0,62rtok от заземлителя. Компьютерная модель позволяет провести серию численных экспериментов по проверке этого для заземлителей самой разной конструкции. Их результаты перед вами (рис. 17-20).
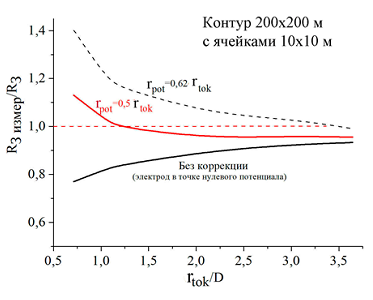
Рисунок 17
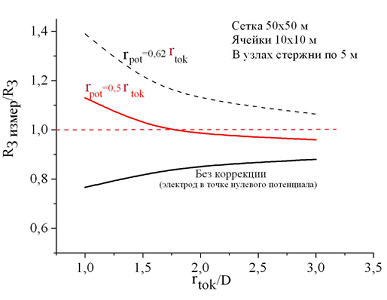
Рисунок 18
Как и следовало ожидать, измерения по точке нулевого потенциала дают заниженные значения сопротивления заземления, хотя относительная погрешность в случае предписанного удаления токового электрода на расстояние rtok ≥ 3D не выходит за пределы 10-12%. Такое вполне допустимо для практики. Измерения при удалении потенциального электрода на расстояние 0,62rtok следует признать перекомпенсированными, хотя при rtok ≥ 3D погрешность также укладывается в 10%.
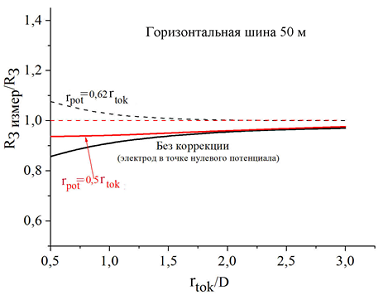
Рисунок 19
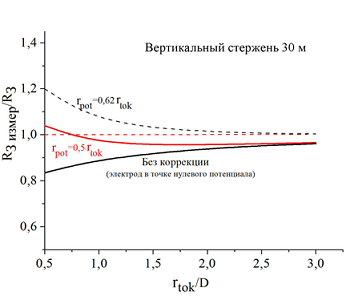
Рисунок 20
Э. М. Базелян, д.т.н., профессор
Энергетический институт имени Г.М. Кржижановского, г. Москва
Читайте далее "Индивидуальный контур заземления – насколько это реально?".
Полезные материалы:
- Серия статей о молниезащите для новичков
- Серия вебинаров о заземлении и молниезащите с профессором Э.М. Базеляном
- Элементы внешней молниезащиты
- Консультации по выбору, проектированию и монтажу систем заземления и молниезащиты
Смотрите также:
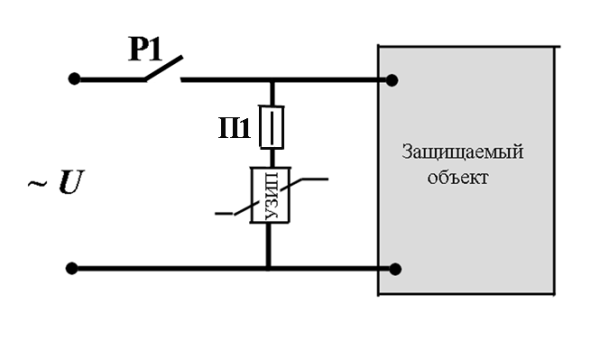 УЗИП и его плавкая вставка
УЗИП и его плавкая вставка
 Молниезащита и заземление для базовых станций стандарта 5G
Молниезащита и заземление для базовых станций стандарта 5G
 Анализ нормативного документа ФЕДЕРАЛЬНЫЕ НОРМЫ И ПРАВИЛА В ОБЛАСТИ ПРОМЫШЛЕННОЙ БЕЗОПАСНОСТИ "ПРАВИЛА БЕЗОПАСНОСТИ ПРИ ВЗРЫВНЫХ РАБОТАХ"
Анализ нормативного документа ФЕДЕРАЛЬНЫЕ НОРМЫ И ПРАВИЛА В ОБЛАСТИ ПРОМЫШЛЕННОЙ БЕЗОПАСНОСТИ "ПРАВИЛА БЕЗОПАСНОСТИ ПРИ ВЗРЫВНЫХ РАБОТАХ"

